Def. av inverterbarhet
Hej!
Hur är det egentligen inverterbara funktioner definieras som?
I min kursbok (Calculus av Adams och Essex) definieras en inverterbar funktion som en funktion som är "one-to-one". Dvs injektiv.
Men min föreläsare har använt två definitioner i två olika kursdelar. Menar han bara att om en funktion är bijektiv, då är det självfallet att den är inverterbar, för då är den ju injektiv?
Det han skriver är följande:
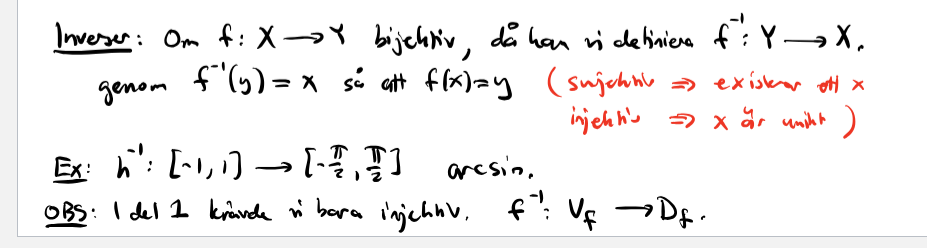
"del 1" avser en kursdel där inversa klassiska funktioner (ln, arccos, arcsin osv.) togs upp. Här kom de upp igen vid ett senare tillfälle och då kom denna nya definition upp.
Gäller båda? Räcker det att den är injektiv?
En funktion måste vara både injektiv och surjektiv för att vara inverterbar. Alltså bijektiv.
Enligt OBS-kommentaren på sista raden, så verkar det att man i kursens del 1 tänkte sig att Y = funktionens värdemängd, men nu (i del 2) är Y = funktionens målmängd.
Om Y=Vf så är f surjektiv per automatik.
Om Y=målmängden, så måste man uttryckligen kräva att f är surjektiv (vilket i sin tur innebär att det faktiskt gäller att Y=Vf)
Om en funktion är injektiv, men inte surjektiv, så kan man krympa målmängden till värdemängden och få en bijektiv funktion. Men om man skall vara strikt så är detta en ny funktion, eftersom definitionen av en funktion brukar innefatta att man fastställer målmängden. Så därför kan man ibland, lite oegentligt, säga att en injektiv funktion är inverterbar.
LuMa07 skrev:Enligt OBS-kommentaren på sista raden, så verkar det att man i kursens del 1 tänkte sig att Y = funktionens värdemängd, men nu (i del 2) är Y = funktionens målmängd.
Om Y=Vf så är f surjektiv per automatik.
Om Y=målmängden, så måste man uttryckligen kräva att f är surjektiv (vilket i sin tur innebär att det faktiskt gäller att Y=Vf)
Just ja, det stämmer bra med vad du säger! Jag funderade också lite själv och drog samma slutsatser. Kursboken jag hänvisar till definierar nog också injektivitet i ett "del 1"-skede, dvs. där man antar att målmängden och värdemängden är samma.
Tack för hjälpen!



