De komplexa talen z1, z2 och z3
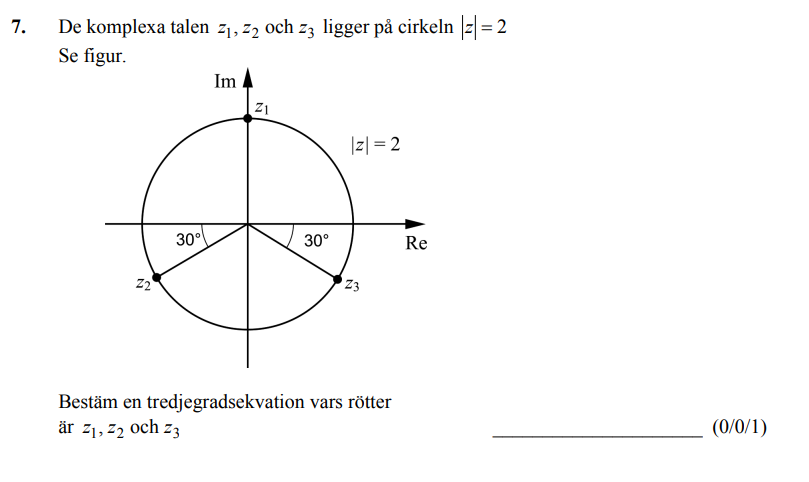
Skulle någon kunna prata mig igenom processen för att hitta svaret här?
Jag ser att perioden borde vara 360/3=120 grader, och att absolute beloppet, alltså r=2. Men jag vet inte exakt hur jag ska gå till väga för att lösa problemet.
Kunde någon ge lite tips? Tack!
Personligen hade jag skrivet ned talen på kvadratisk form, dvs Z=a+ib.
Därefter kan du multiplicera tre faktorer (z-z1)(z-z2)(z-z3) där z1, z2, z3 är dina tal för att erhålla en tredjegradsekvation med z1, z2 och z3 som rötter.
EDIT: Ekvationen blir naturligtvis (z-z1)(z-z2)(z-z3)=0
Ahhhh, okej. Men då får vi inte fram en exakt ekvation? Skulle det fortfarande vara ett acceptabelt svar på frågan?
Eller, på polär form
z3 = r*eiv
återstår att bestämma r och v, som enklast görs genom att använda reglerna för multiplikation av komplexa tal och deras absolutbelopp och argument
r=23
v är summan av de tre argumenten för z, dvs 90+210-30 = 270
Om du vill kan du sen gå tillbaka till rektangulär form, vinkeln 270 har ju snälla värden för sin och cos.
z3 = 23(cos(270)+i*sin(270))




