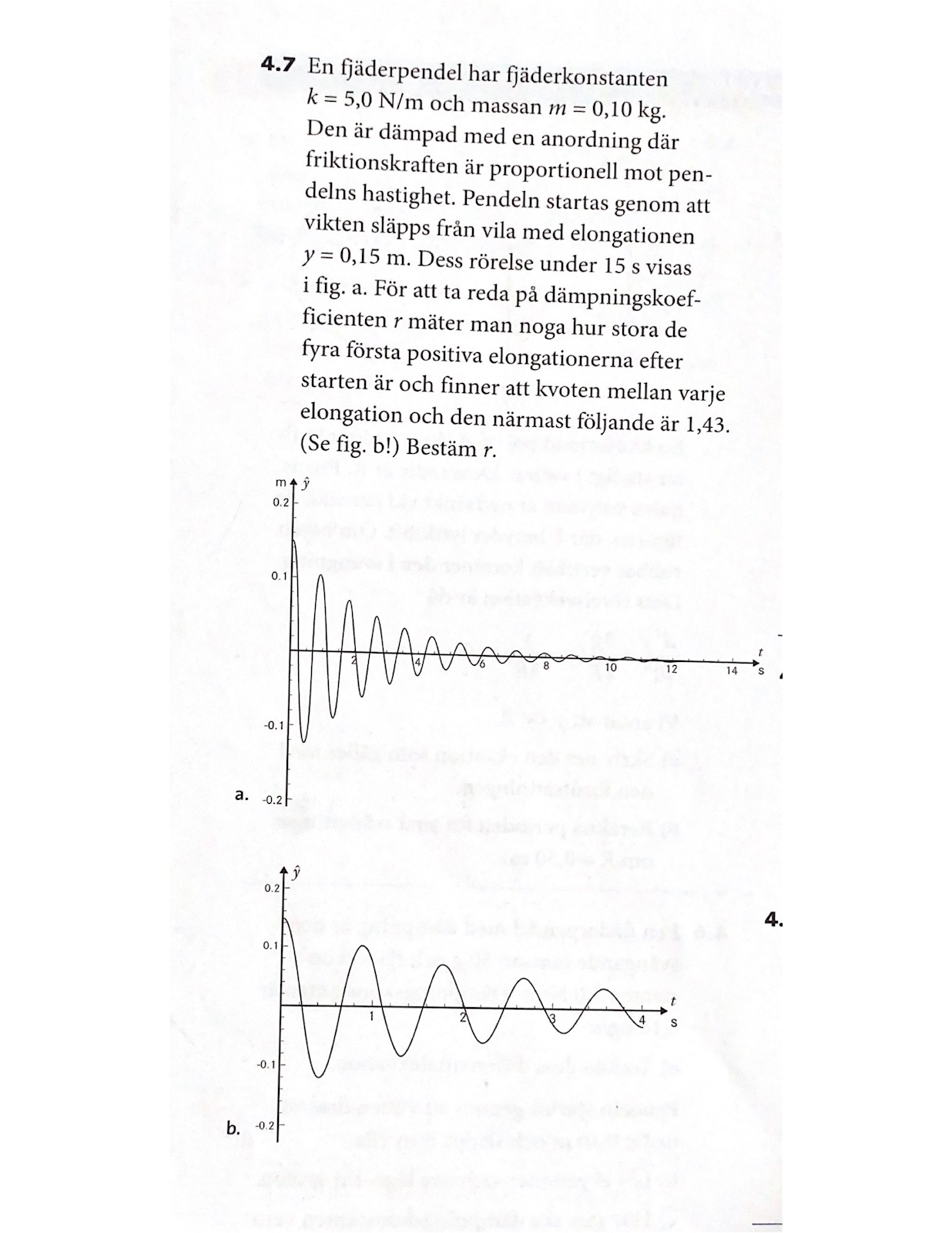
dämpad harmonisk svägning, bestämma dämpningskonstanten


vad är det jag missar???
fysik3 skrev:
vad är det jag missar???
Allt som behövs är att bestämma dämpningskoefficienten r utifrån det förhållandet.
Om denna kvot hade varit 1 hade det blivit
Vad är det som du tycker inte stämmer?
Snarare än att försöka hitta ett analytiskt uttryck för svängningsrörelsen som funktion av t (du borde sätta y(0)= 0.15 där, men det hjälper dig inte så mycket eftersom det blir ändå ganska komplicerat), så ska du förmodligen som Pieter säger koncentrera dig på den dämpade delen av rörelsen.
Och sedan approximativt avläsa den data du behöver ur grafen..
Annars hade det inte funnits någon anledning att zooma in grafen i uppgifttexten. Men man borde även kunna räkna fram r på det sättet du försöker, utan att göra någon ytterligare avläsning i grafen än vad som står i uppgifttexten.
JohanF skrev:Och sedan approximativt avläsa den data du behöver ur grafen..
Annars hade det inte funnits någon anledning att zooma in grafen i uppgifttexten.
Visst, det är konstigt. Men kanske är det en kvarleva från en tidigare version av uppgiften. Nu står det i uppgiftstexten att kvoten mellan svängningarna är 1,43.
Det leder direkt till ett värde för systemets Q-faktor och sedan också till dämpningskoefficienten.
Jag förstår inte riktigt hur jag ska använda informationen om att "kvoten mellan varje elongation och den närmast följande är 1,43".
Finns det något samband mellan dämpningskonstantenn och elongationen? Eller är det något jag missar i uppgiften? För jag vet att följande samband gäller γ
Pieter Kuiper skrev:fysik3 skrev:
vad är det jag missar???
Allt som behövs är att bestämma dämpningskoefficienten r utifrån det förhållandet.
Om denna kvot hade varit 1 hade det blivit
hur vet jag det?
fysik3 skrev:Finns det något samband mellan dämpningskonstanten och elongationen?
Nej, men om dämpningen är noll är amplituden konstant (så kvoten som uppgiften talar om är då 1). Det är odämpad fri svängning.
Om amplituden minskar är dämpningskoefficienten större än noll. Sedan får du nog kolla vad boken exakt menar med dämpningskoefficienten, det finns lite olika termer och definitioner i literaturen: dämpningskonstanten, dämpningskoefficienten, dämpningsförhållandet.
En vanlig beteckning är . Här en figur som leder till en uppskattning av denna zeta:
https://commons.wikimedia.org/wiki/File:2nd_Order_Damping_Ratios.svg
Pieter Kuiper skrev:JohanF skrev:Och sedan approximativt avläsa den data du behöver ur grafen..
Annars hade det inte funnits någon anledning att zooma in grafen i uppgifttexten.
Visst, det är konstigt. Men kanske är det en kvarleva från en tidigare version av uppgiften. Nu står det i uppgiftstexten att kvoten mellan svängningarna är 1,43.
Det leder direkt till ett värde för systemets Q-faktor och sedan också till dämpningskoefficienten.
Du har kanske rätt Pieter, jag tänkte nog inte hela vägen och blev lite förvirrad av den extra informationen (tänkte att man behövde informationen om periodtiden också)
Jag tror kanske att en godtagbar lösning av uppgiften beror på i vilken kurs den ges. Ges den i kursen fysik 3 på gymnasiet där man behandlar dämpad harmonisk rörelse mer översiktligt så kanske man tillåts få lite hjälp genom att läsa av grafen ändå. Jag tycker grafen ser väldigt tillrättalagd ut för att man ska kunna räkna ut ett bra närmevärde på periodtiden genom att läsa av tiden för fyra svängningsperioder. Det kan inte gärna vara ett misstag att man har zoomat in på det där sättet. Annars går den ju att lösa även enbart med texten.
Ges uppgiften på fysik3 på gymnasiet?
JohanF skrev:Jag tror kanske att en godtagbar lösning av uppgiften beror på i vilken kurs den ges. Ges den i kursen fysik 3 på gymnasiet där man behandlar dämpad harmonisk rörelse mer översiktligt så kanske man tillåts få lite hjälp genom att läsa av grafen ändå. Jag tycker grafen ser väldigt tillrättalagd ut för att man ska kunna räkna ut ett bra närmevärde på periodtiden genom att läsa av tiden för fyra svängningsperioder. Det kan inte gärna vara ett misstag att man har zoomat in på det där sättet. Annars går den ju att lösa även enbart med texten.
Ges uppgiften på fysik3 på gymnasiet?
ja
Men du kan istället för att avläsa T ur grafen, också ha utnyttjat sambandet mellan gamma och vinkelhastigheten omega (och därmed periodtiden) som du skrev med rött i TS.





