Dammen - omfångsrika problemsituationer (Matematik/Matte 5)

bump

Jag kom fram till en lösning till uppgift c, men efter att ha läst uppgift d) så är jag osäker ifall det är rätt.

Efter att ha undersökt hur verkliga dammvallar ser ut verkar det som att de är sne/böjda för att minska det hydrostatiska trycket, men mitt svar till uppgift c) verkar visa motsatsen. Betyder det att jag har räknat fel eller betyder det att matten jag använde inte kan appliceras till en verklig scenario?

Jag tror att du tänker rätt vid uträkningen, och får ut rätt svar (tror jag). Du behöver bara snygga till mattespråket i uppställningen lite (du glömde $d x$ ända fram till ledet med integraltecknet. Säkert bara ett slarvfel).

På ett areaelement $d A$ av dammvallen så verkar kraften

$d F = ρ g h \cdot d A = ρ g h \cdot 150 d x = ρ g \cdot 75 \sqrt{3} x d x F = \int d F = \int ρ g \cdot 75 \sqrt{3} x d x . . .$

Har du läst att de riktiga dammvallarna är sneda/böjda _för att_ minska det hydrostatiska trycket på dem? Eller skulle de kunna vara sneda/böjda av någon annan anledning?

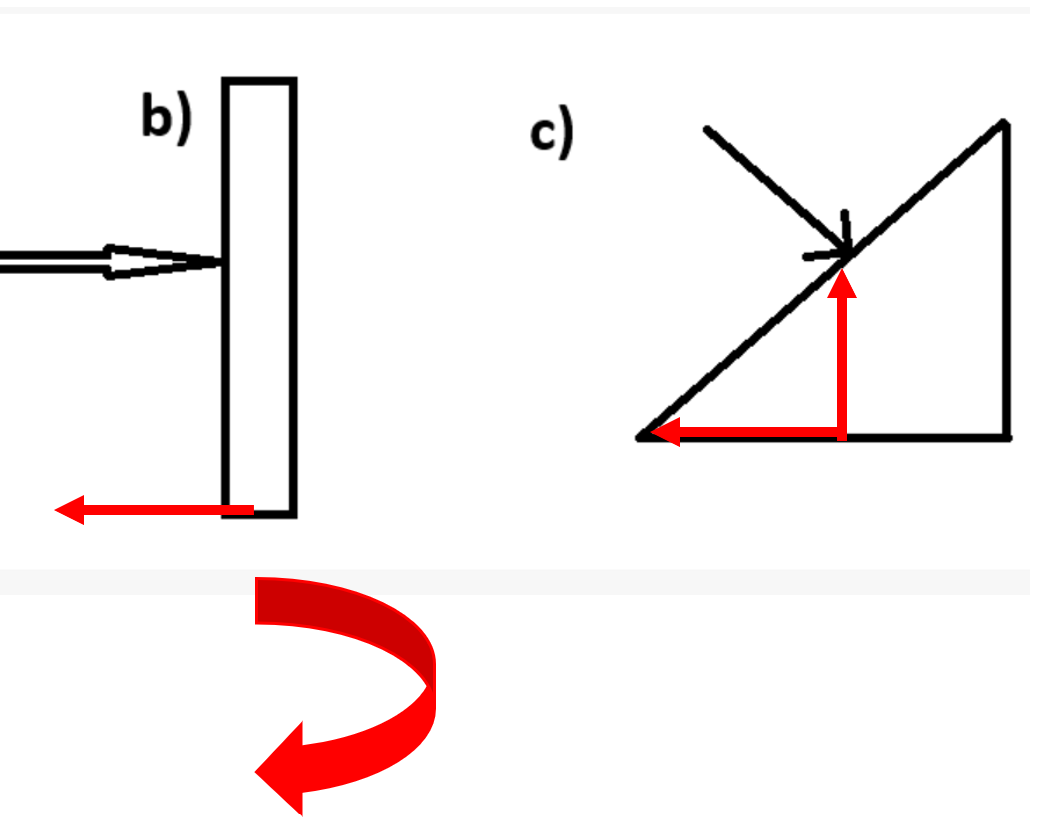
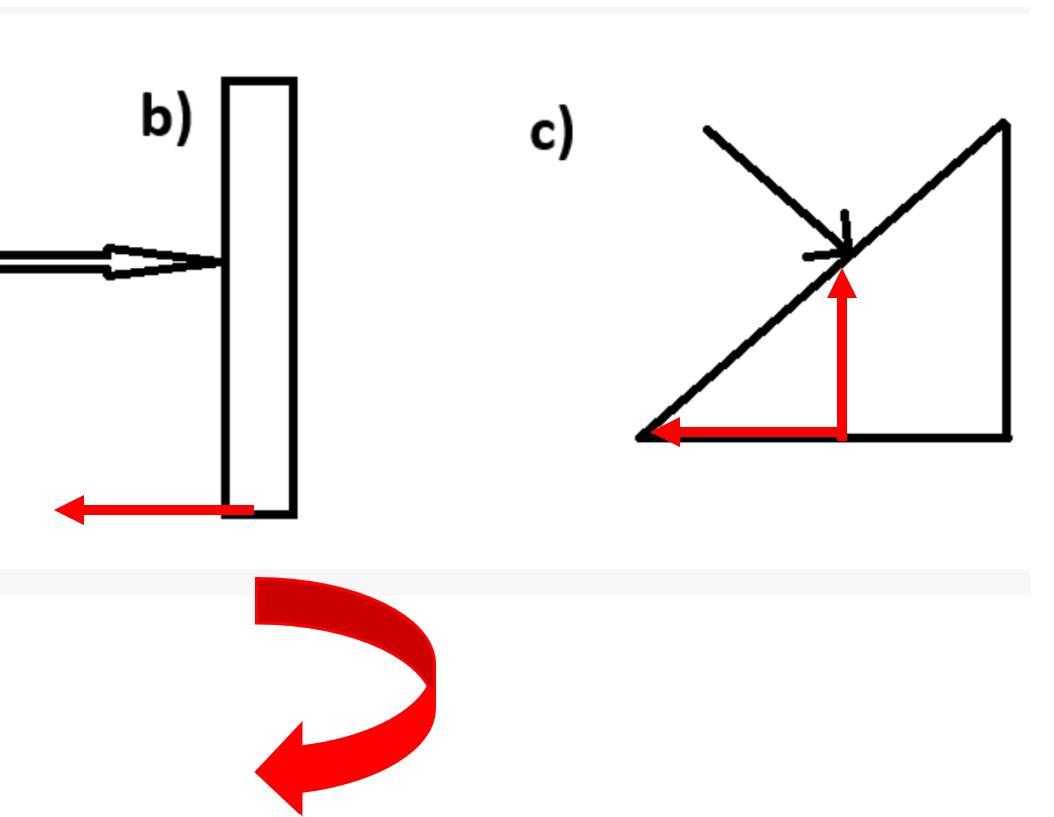
I vilken riktning verkar kraften som du har räknat ut i b respektive c?

JohanF skrev:
Jag tror att du tänker rätt vid uträkningen, och får ut rätt svar (tror jag). Du behöver bara snygga till mattespråket i uppställningen lite (du glömde $d x$ ända fram till ledet med integraltecknet. Säkert bara ett slarvfel).

På ett areaelement $d A$ av dammvallen så verkar kraften

$d F = ρ g h \cdot d A = ρ g h \cdot 150 d x = ρ g \cdot 75 \sqrt{3} x d x F = \int d F = \int ρ g \cdot 75 \sqrt{3} x d x . . .$

Ska man verkligen ha dx innan man integrerar? Borde inte det komma efter man integrerar båda sidor?

Har du läst att de riktiga dammvallarna är sneda/böjda _för att_ minska det hydrostatiska trycket på dem? Eller skulle de kunna vara sneda/böjda av någon annan anledning?

Det var egentligen bara en hypotes eftersom de flesta bilderna på dammar jag hittade verkar vara sneda/böjda, men det skulle kunna finnas en annan anledning. Tyvärr har jag inte lyckats hitta mycket information om varför de är sneda/böjda...

I vilken riktning verkar kraften som du har räknat ut i b respektive c?

Så här tror jag att de är riktade: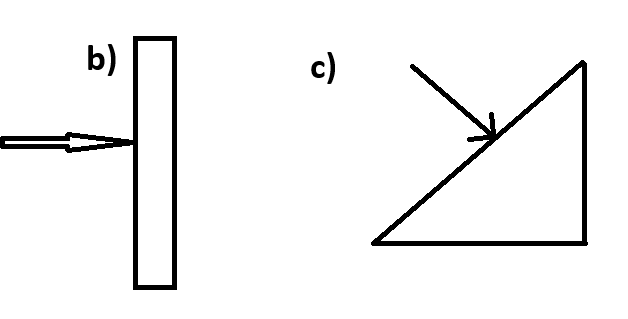

Korrigering till mitt förra meddelande: Min lösning visar att den hydrostatiska kraften är densamma, inte det hydrostatiska trycket.

tahlas05 skrev:
JohanF skrev:
Jag tror att du tänker rätt vid uträkningen, och får ut rätt svar (tror jag). Du behöver bara snygga till mattespråket i uppställningen lite (du glömde $d x$ ända fram till ledet med integraltecknet. Säkert bara ett slarvfel).

På ett areaelement $d A$ av dammvallen så verkar kraften

$d F = ρ g h \cdot d A = ρ g h \cdot 150 d x = ρ g \cdot 75 \sqrt{3} x d x F = \int d F = \int ρ g \cdot 75 \sqrt{3} x d x . . .$

Ska man verkligen ha dx innan man integrerar? Borde inte det komma efter man integrerar båda sidor?

Har du läst att de riktiga dammvallarna är sneda/böjda _för att_ minska det hydrostatiska trycket på dem? Eller skulle de kunna vara sneda/böjda av någon annan anledning?

Det var egentligen bara en hypotes eftersom de flesta bilderna på dammar jag hittade verkar vara sneda/böjda, men det skulle kunna finnas en annan anledning. Tyvärr har jag inte lyckats hitta mycket information om varför de är sneda/böjda...

I vilken riktning verkar kraften som du har räknat ut i b respektive c?

Så här tror jag att de är riktade:

Vad jag fann på nätet är trycket alltid vinkelrätt. Vad man kan säga är att med lägre lutning blir x-komposanten mindre, vilket minskar trycket på konstruktionen. Men jag är ingen ingenjör…

Kraften tycker jag borde vara riktad som tahlas05 ritar. Blir det någon fördel för dammväggens förmåga att stå emotkraften från vatten massorna?

Trinity2 skrev:
tahlas05 skrev:
JohanF skrev:
Jag tror att du tänker rätt vid uträkningen, och får ut rätt svar (tror jag). Du behöver bara snygga till mattespråket i uppställningen lite (du glömde $d x$ ända fram till ledet med integraltecknet. Säkert bara ett slarvfel).

På ett areaelement $d A$ av dammvallen så verkar kraften

$d F = ρ g h \cdot d A = ρ g h \cdot 150 d x = ρ g \cdot 75 \sqrt{3} x d x F = \int d F = \int ρ g \cdot 75 \sqrt{3} x d x . . .$

Ska man verkligen ha dx innan man integrerar? Borde inte det komma efter man integrerar båda sidor?

Ja! Det ska du (du har själv gjort det på a-uppgiften). Varför skulle du plötsligt multiplicera med dx eller dh i högerledet när du inte gör det i vänsterledet?

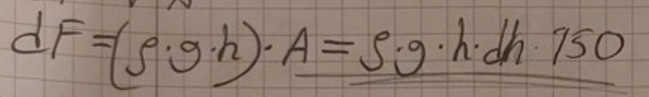
För att du ska kunna integrera både högerled och vänsterled, så måste du ha en differential i både högerled och vänsterled.

VL integreras för att summera alla kraftdifferentialer

$F = \int d F$

...och då måste också vänsterledet integreras

$\int . . . d x$

Eller, titta på storheterna. Vänsterledet $d F$ är en $k r a f t$ . Då måste högerledet också vara en $k r a f t$ eller $t r y c k \cdot a r e a$ .

Den längd på triangeln som jag kallar x, är det den som egentligen ska vara dx?

Blir det någon fördel för dammväggens förmåga att stå emotkraften från vatten massorna?

Jag vet faktiskt inte.

Jag provade att kolla om trycket blev mindre, men det verkar som att den blir samma som i uppgift b):

Uppgift b tryck:
p = (998*9.82*150*72) / (150*12) = 58802.16 Pa

Uppgift c tryck:

p = (998*9.82*√3*75*((24/√3)^2)/2) / ( 150*(24/√3)) = 58802.16 Pa

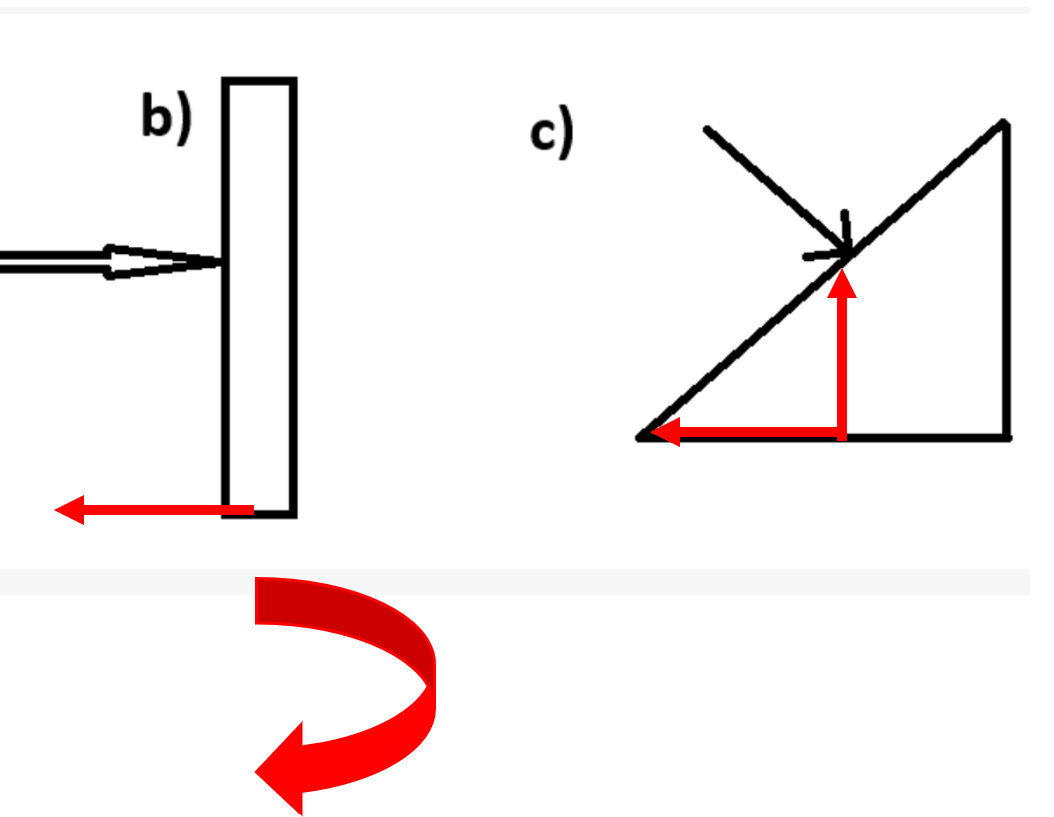
Jag har ritat in några krafter som dammvallarnas fästpunkter i marken måste utöva på damvallarna för att de ska kunna stå emot kraften från vattnet (det är lite fel skala eftersom kraften i c är större än i b, men det spelar ingen större roll för resonemanget)

Titta på b. Ett litet betongfundament som sitter fast i marken måste hålla emot allt kraften från vattnet. Dessutom blir det ett stor vridmoment på fundamentet som det måste stå pall för.

Varför blir konstruktionen i c stabilare, tror du?

Kan något hjälpa mig med en uppgift

JohanF skrev:
Jag har ritat in några krafter som dammvallarnas fästpunkter i marken måste utöva på damvallarna för att de ska kunna stå emot kraften från vattnet (det är lite fel skala eftersom kraften i c är större än i b, men det spelar ingen större roll för resonemanget)

Titta på b. Ett litet betongfundament som sitter fast i marken måste hålla emot allt kraften från vattnet. Dessutom blir det ett stor vridmoment på fundamentet som det måste stå pall för.

Varför blir konstruktionen i c stabilare, tror du?

Beror det på att kraften kan delas upp i flera komposanter? I b är kraftkomposanten i y-led noll, medan i c kan kraften delas in i en komposant i x och y (och deras storlek är hälften av vattnets kraft som är horisontellt med planet).

Hejochtack skrev:
Kan något hjälpa mig med en uppgift

Jag tror att det är bättre om du skapar din egen tråd och förklarar vad du behöver hjälp med.

tahlas05 skrev:
JohanF skrev:
Jag har ritat in några krafter som dammvallarnas fästpunkter i marken måste utöva på damvallarna för att de ska kunna stå emot kraften från vattnet (det är lite fel skala eftersom kraften i c är större än i b, men det spelar ingen större roll för resonemanget)

Titta på b. Ett litet betongfundament som sitter fast i marken måste hålla emot allt kraften från vattnet. Dessutom blir det ett stor vridmoment på fundamentet som det måste stå pall för.

Varför blir konstruktionen i c stabilare, tror du?

Beror det på att kraften kan delas upp i flera komposanter? I b är kraftkomposanten i y-led noll, medan i c kan kraften delas in i en komposant i x och y (och deras storlek är hälften av vattnets kraft som är horisontellt med planet).

Det stämmer. Jämför med att köra upp en bil på en ramp. Är det rampen nästan horisontal påverkas den inte mycket av bilens hjul. Ju brantare rampen är, ju mer vill bilens hjul föra rampen framåt.

Ju flackare damm, desto mindre tryck på konstruktionen.

Detta används vid skydd mot översvämning i mindre skala

https://hallbyggarna.se/bygga-skydd-mot-oversvamningar-med-presenningar/

tahlas05 skrev:
JohanF skrev:
Jag har ritat in några krafter som dammvallarnas fästpunkter i marken måste utöva på damvallarna för att de ska kunna stå emot kraften från vattnet (det är lite fel skala eftersom kraften i c är större än i b, men det spelar ingen större roll för resonemanget)

Titta på b. Ett litet betongfundament som sitter fast i marken måste hålla emot allt kraften från vattnet. Dessutom blir det ett stor vridmoment på fundamentet som det måste stå pall för.

Varför blir konstruktionen i c stabilare, tror du?

Beror det på att kraften kan delas upp i flera komposanter? I b är kraftkomposanten i y-led noll, medan i c kan kraften delas in i en komposant i x och y (och deras storlek är hälften av vattnets kraft som är horisontellt med planet).

Bra! och vad bra med exempel från verkligheten! (det är vektoraddition, så krafterna blir inte hälften så stora).

Så en fördel är alltså att vattenmassorna trycker fast dammväggen mot underlaget så att friktionen ökar och förhindrar dammvallen från att glida iväg. Nästa fördel är angående vridmomentet som dammvallen utsätts för. Eftersom den vertikala kraften från vattnet på dammvallen ökar ju djupare ner i vattnet man kommer, så kommer motsols vridmomentet på vallen att balansera det medsols vridmoment som den horisontella kraftkomposanten skapar högre upp på dammvallen.

Det viktiga med konstruktionen är alltså att dammvallen är tillräckligt styv, vilket åstadkoms med stålprofilerna i länken.

Den längd på triangeln som jag kallar x, är det den som egentligen ska vara dx?

Såhär:

Väsketrycket på vattendjupet $h$ är fortfarande $ρ g h$ (såklart) i uppgift c. Men till skillnad från det som beskrivs i uppgifttexten, så är inte längre tjockleken på "remsan" $d h$ , utan $d x$ . Längden på remsan vid djupet $h$ med konstant tryck är, fortfarande 150m lång. Alltså:

På ett areaelement ("remsan") $d A$ av dammvallen så verkar kraften

$d F = ρ g h \cdot d A = ρ g h \cdot 150 d x = ρ g \cdot 75 \sqrt{3} x d x$

Dock är ju högerledet fortfarande svår att integrera utan att känna sambandet mellan h och x. Detta samband kan man få ur triangeln ,som du listade ut:

$h = x \cdot \cos 30^{°} = \frac{\sqrt{3}}{2} x$

Alltså:

$d F = ρ g h \cdot d A = ρ g h \cdot 150 d x = ρ g \cdot 75 \sqrt{3} x d x F = \int d F = \int ρ g \cdot 75 \sqrt{3} x d x . . .$

JohanF skrev:

Den längd på triangeln som jag kallar x, är det den som egentligen ska vara dx?

Såhär:

Väsketrycket på vattendjupet $h$ är fortfarande $ρ g h$ (såklart) i uppgift c. Men till skillnad från det som beskrivs i uppgifttexten, så är inte längre tjockleken på "remsan" $d h$ , utan $d x$ . Längden på remsan vid djupet $h$ med konstant tryck är, fortfarande 150m lång. Alltså:

På ett areaelement ("remsan") $d A$ av dammvallen så verkar kraften

$d F = ρ g h \cdot d A = ρ g h \cdot 150 d x = ρ g \cdot 75 \sqrt{3} x d x$

Dock är ju högerledet fortfarande svår att integrera utan att känna sambandet mellan h och x. Detta samband kan man få ur triangeln ,som du listade ut:

$h = x \cdot \cos 30^{°} = \frac{\sqrt{3}}{2} x$

Alltså:

$d F = ρ g h \cdot d A = ρ g h \cdot 150 d x = ρ g \cdot 75 \sqrt{3} x d x F = \int d F = \int ρ g \cdot 75 \sqrt{3} x d x . . .$

Jag förstår fortfarande inte riktigt vart dx kommer från. Jag trodde att den lilla triangeln skulle representera remsan och därför är remsans area dA = 150*x

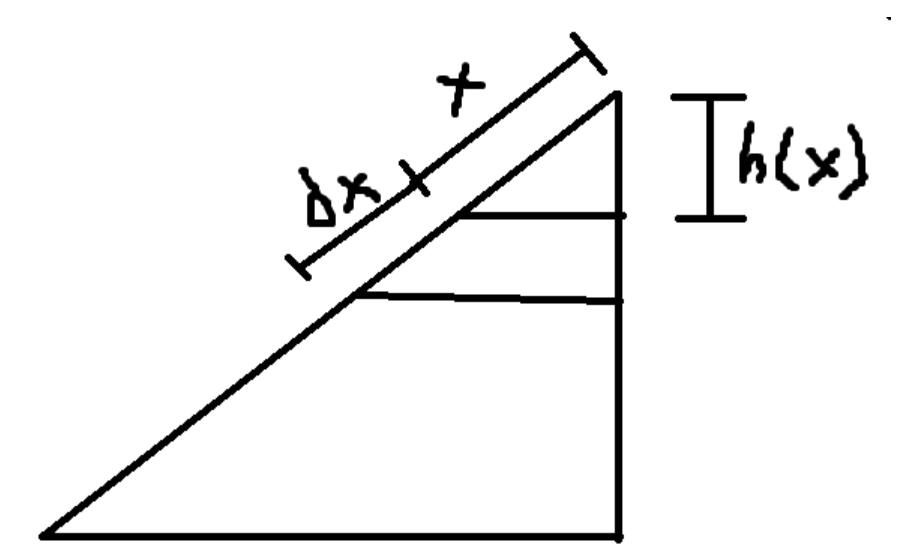
Är det så här du tänker?:
dx är tjockleken på remsan, x ger längden från toppen av vallen till remsan (parallellt med planet) och h(x) ger längden från toppen av vallen till remsan (lodrätt).

Ungefär såhär tänker jag:

- Först tänker jag för att få grepp om hur problemet ser ut, lite enklare. Hmm, hur skulle det ha sett ut om trycket mot den sluttande dammvallen hade varit konstant, säg $P_{0}$ , över hela dammvallsytan. Jo, enkelt, $F = P_{0} \cdot A$ , där $A$ är dammvallsytan $150 \cdot \frac{24}{\sqrt{3}} m^{2}$

- Sedan tänker jag, OK, men om nu trycket varierar med vattendjupet, hur gör jag då? Då kan jag ju inte direkt multiplicera arean med trycket, eftersom olika delar av ytan har olika tryck. Då måste jag försöka hitta någon form av litet areaelement som är så litet så att det har konstant tryck, och sedan integrera ihop alla dessa små areaelement som utgör hela ytan, multiplicerat med "sitt" tryck, så kommer jag att få den totala kraften $F$

- Jag ser att tack vare symmetrin så kan detta lilla areaelement med konstant tryck, vara en tunn remsa med längden $150 m$ och tjockleken $d x$ , och om jag sedan integrerar mellan $x = 0$ och $x = \frac{24}{\sqrt{3}}$ , så har jag täckt hela ytan.

Alltså

$A = \int_{0}^{\frac{24}{\sqrt{3}}} 150 d x F = \int_{0}^{\frac{24}{\sqrt{3}}} ρ g h \cdot 150 d x$

men eftersom $h$ beror av $x$ ,så måste jag uttrycka $h$ som en funktion av $x$ närj ag integrerar. Alltså:

$F = \int_{0}^{\frac{24}{\sqrt{3}}} ρ g \cdot \frac{\sqrt{3} x}{2} \cdot 150 d x$

Jag har försökt beskriva det på ett lite annat sätt här ovan, men jag upprepar mig en hel del tror jag. Fortsätt bara fråga.

Din figur tycker jag ser bra ut, men x'et kan du ta bort, det tillför inget. Att det finns med ett x i integralen som beräknas är enbart eftersom h måste vara uttryckt i x, för att kunna beräkna integralen.

Din figur tycker jag ser bra ut, men x'et kan du ta bort, det tillför inget. Att det finns med ett x i integralen som beräknas är enbart eftersom h måste vara uttryckt i x, för att kunna beräkna integralen.

Men hur ska jag få uttrycket h(x) om jag tar bort x'et? Jag har ju använt trigonometri för att få h(x).

Jag uttryckte mig nog lite slarvigt. Ur "fysikförståeleperspektiv" så tillför den inte mycket eftersom sträckan x inte är en okänd sträcka som vi ska räkna ut i uppgiften, utan i det här fallet är x en integrationsvariabel.

Jag hade kanske ritat en koordinataxel x i den riktningen istället, så hade det kanske blivit tydligt vad som menats (men det förstår man ändå, eftersom dx är ditritad)

JohanF skrev:
Jag uttryckte mig nog lite slarvigt. Ur "fysikförståeleperspektiv" så tillför den inte mycket eftersom sträckan x inte är en okänd sträcka som vi ska räkna ut i uppgiften, utan i det här fallet är x en integrationsvariabel.

Jag hade kanske ritat en koordinataxel x i den riktningen istället, så hade det kanske blivit tydligt vad som menats (men det förstår man ändå, eftersom dx är ditritad)

Jaha, okej. Tack nu förstår jag!

Bra jobbat! (Speciellt bra att du inte gav upp i början...)