Cosinussatsen
Frågan lyder följande :
I den likbenta triangeln ABC är sidorna AB och BC 10 cm. Sidan AC är 12 cm. En punkt D sätts ut på BC så att AD blir 10.5 cm. Beräkna vinklarna i triangeln ABD.
Jag tolkade AD som ett sträck ner åt så det blidas 2 mindre vinklar med 90 grader men det var fel. Jag antar att jag inte förstår vad de menar med "En punkt D sätts ut på BC så att AD blir 10.5 cm."
Hoppas du ritat en bild, annars är detta omöjligt:) skicka bild på din uträkning
Iyed02 skrev:
:Jag antar att jag inte förstår vad de menar med "En punkt D sätts ut på BC så att AD blir 10.5 cm."
Så hör:

Yngve skrev:
Enastående🥹
Yes det var så jag gjorde men fick något helt annat än facit. 
Iyed02 skrev:Yes det var så jag gjorde men fick något helt annat än facit.
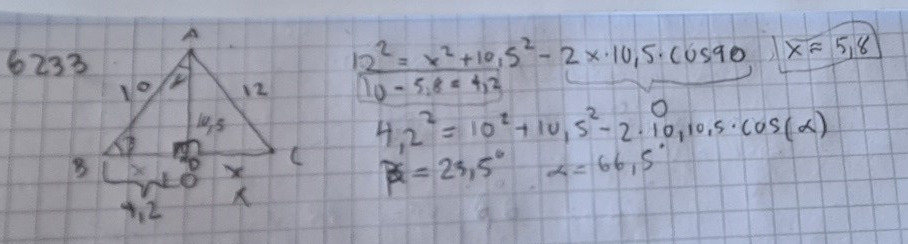
Det hade räckt med alldeles vanlig Pythagoras sats, eftersom du har en rät vinkel. Vad får du för värde på x när du löser Pythagoras-ekvationen?
Varifrån får du värdet 5,8? Det kan inte vara från cosinussatsen, eftersom "den krångliga termen" är lika med 0.
EDIT: Det står inte att vinkeln är 90o (jag lurades av den blåa punkten i Yngves bild).
Iyed02 skrev:Yes det var så jag gjorde men fick något helt annat än facit.
I din uträkning så räknar du med att vinkeln ADC är 90°. Hur kom du fram till det?
Jag gjorde så nu men facit är: 40,66,74 grader. Har försökt göra om men får inte ett närmare värde.
Visa spoiler
Skriv ditt dolda innehåll här
Det är lite svårt att följa dina tankegångar.
Hur kom du fram till det blåmarkerade, dvs att x = 2,2?

Gjorde om den, är det tydligare nu? Tack för hjälpen!





