cos(x + 60⁰) - cos(x-60⁰)???????
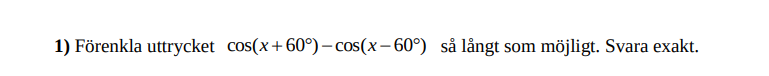
Hur beräknar man sådant uppgifter.....?
Tack för all hjälp..
Hej.
Titta I din formelsamling efter additionsformler för cosinus.
Hittar du något intressant?
Här?

ii_noor06 skrev:
Ja. Välj någon som passar.
Vad ska jag göra sen...förstår ej---
ii_noor06 skrev:Vad ska jag göra sen...förstår ej---
Skriv om termen cos(x+60°) med hjälp av formel #3.
Skriv om termen cos(x-60°) med hjälp av formel #4.
Visa hur uttrycket ser ut då.
Titta sedan i ditt formelblad efter exakta värden på cos(60°) och sin(60°).
cos( x + 60⁰ ) = cos ( x ) cos ( +60⁰ ) − sin(x)sin(y) ingen aning här...
cos ( x - 60⁰ ) = cos ( x ) cos ( -60⁰ ) + sin ( x ) sin ( y ) Förstår ej här heller....
Jag vet det är fel men problemet är som jag sa tidigare jag studerar distans och när jag skickar till lärarna så svarar de inte... och ifall de svarar så säger de skriv ett gmail till nån mattehjälpare .... hotmail.com där nån matte lärare svarar... jag har skickat flera gånger till de och får inget svar av någon--- så jag ligger jätte efter med matten.... så vet inte hur det ska gå till.
Försöker kolla på YT o så men för att jag inte vet hur man gör så förstår jag inte vad de försöker förmedla...
Du vill förenkla uttrycket cos(x+60o)-cos(x-60o)så mycket som möjligt.
Du har hittat formlerna cos(a+b) = cos(a)cos(b)-sin(a)sin(b)
och cos(a-b)= cos(a)cos(b)+sin(a)sin(b).
Om vi sätter x respektive 60o får vi cos(x+60o) = cos(x)cos(60o)-sin(x)sin(60o)
och cos(x-60o)= cos(x)cos(60o)+sin(x)sin(60o).
Subtraherar vi den med minus (från början) från den med plus får vi cos(x)cos(60o)-sin(x)sin(60o) -(cos(x)cos(60o)+sin(x)sin(60o)).
Tar vi bort parentesen och byter tecken där det behövs blir det cos(x)cos(60o)-sin(x)sin(60o) -cos(x)cos(60o)-sin(x)sin(60o).
Ser du att två av termerna kommer att ta ut varandra? Vad blir det kvar när du har förenkklat?
cos(x)cos(60⁰)-sin(x)sin(60⁰)-cos(x)cos(60⁰)-sin(x)sin(60⁰)
cos(x)cos(60⁰)-cos(x)cos(60⁰)=0
-sin(x)sin(60⁰)- sin(x)sin(60⁰) = sin(x)sin(60⁰)
Kvar: sin(x)sin(60⁰)
Eller?
ii_noor06 skrev:cos(x)cos(60⁰)-sin(x)sin(60⁰)-cos(x)cos(60⁰)-sin(x)sin(60⁰)
cos(x)cos(60⁰)-cos(x)cos(60⁰)=0
Ja.
-sin(x)sin(60⁰)- sin(x)sin(60⁰) = sin(x)sin(60⁰)
Nej. Vi tar ett enklare exempel: -a-a = ?
Kvar: sin(x)sin(60⁰)
Eller?
Nej.
Nej. Vi tar ett enklare exempel: -a-a = ?
-2a
Så blir svaret __:
-sin(x)sin(60⁰)-sin(x)sin(60⁰) = 2( sin(x)sin(60⁰) )
Vart tog minustecknet vägen?
mrpotatohead skrev:Vart tog minustecknet vägen?
Ojj,
Så. -2(sin(x)sin(60⁰)) eller -2(sin(x)sin(60⁰))
ii_noor06 skrev:
Ojj,
Så. -2(sin(x)sin(60⁰)) eller -2(sin(x)sin(60⁰))
Ja, det stämmer..
Nu kan du ersätta sin(60°) med ett exakt värde.
Titta i ditt formelblad om du inte kan det utantill.
Märkte nyss att jag skrev två likadana uttryck fast jag än tänkte på två olika...
Rätt?
Nepp. Du ska byta hela uttrycket, inte vinkeln
mrpotatohead skrev:Nepp. Du ska byta hela uttrycket, inte vinkeln
Hur ska jag göra det?
Där det står sin(60) sätter du in (roten ur 3)/2
ii_noor06 skrev:Märkte nyss att jag skrev två likadana uttryck fast jag än tänkte på två olika...
... och båda var rätt 😀👍
Yngve skrev:
... och båda var rätt 😀👍
Ja hahah jag råkade skriva det....
mrpotatohead skrev:Där det står sin(60) sätter du in (roten ur 3)/2
Vad det inte det jag gjorde?
Eller ska det vara så här,
-2(sin(x)))
ii_noor06 skrev:
Vad det inte det jag gjorde?
Nej
Eller ska det vara så här,
-2(sin(x)))
Ja, så ska det vara, och det uttrycket kan förenklas.
Vad ska jag göra sedan?
ii_noor06 skrev:Vad ska jag göra sedan?
Förenkla uttrycket
Du har en tvåa, och en tvåa i nämnaren. Förenkla det! och roten-ur-tre är ett exakt tal, avrunda det inte!
Smaragdalena skrev:Du har en tvåa, och en tvåa i nämnaren. Förenkla det! och roten-ur-tre är ett exakt tal, avrunda det inte!
Min räknare på datan säger att roten ur tre blir 1.73205080757.
Är det fel?
Och när jag tog det delat på 2 fick jag svaret 0.866025403784.
ii_noor06 skrev:Smaragdalena skrev:Du har en tvåa, och en tvåa i nämnaren. Förenkla det! och roten-ur-tre är ett exakt tal, avrunda det inte!
Min räknare på datan säger att roten ur tre blir 1.73205080757.
Är det fel?
Och när jag tog det delat på 2 fick jag svaret 0.866025403784.
Det är inte fel, men det är (tillskilnad från ) inte exakt.
Vad är det exakta talet då?
För jag sökte runt och gav mig exakt samma svar som jag nämnde innan.
Det exakta talet är , så svaret på din uppgift är .
Hur omvandlade du detta
till detta
Smaragdalena skrev:
Ahaa tack så mycket!





