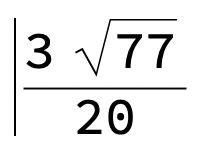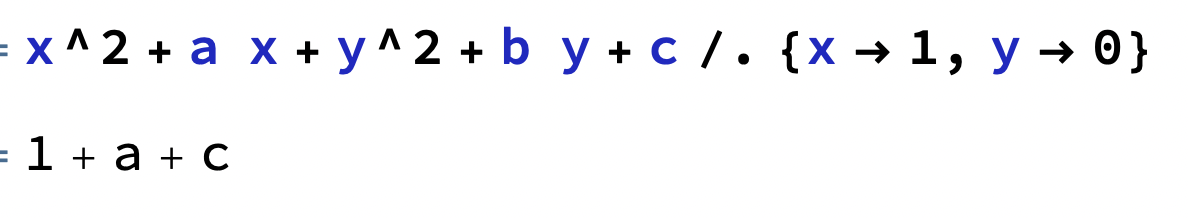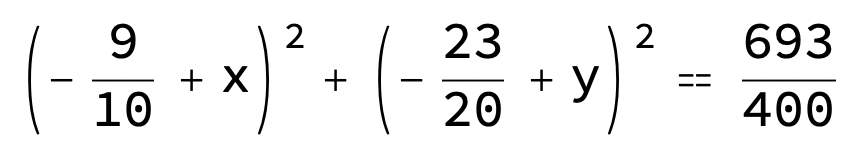Cirkelns radie och medelpunkt och rita en skiss.
Detta är uppgiften

Jag har lyckats lösa första delen av uppgiften med minsta kvadrat metoden, här är min lösning:

ser det bra ut? och min fråga är hur gör jag för att hitta cirkelns radie och medelpunkt?
den andra ekvationen i linjära ekvationerna ska korrigeras.
Den 1:a är rätt, 2:a fel
Trinity2 skrev:Den 1:a är rätt, 2:a fel
Hur?
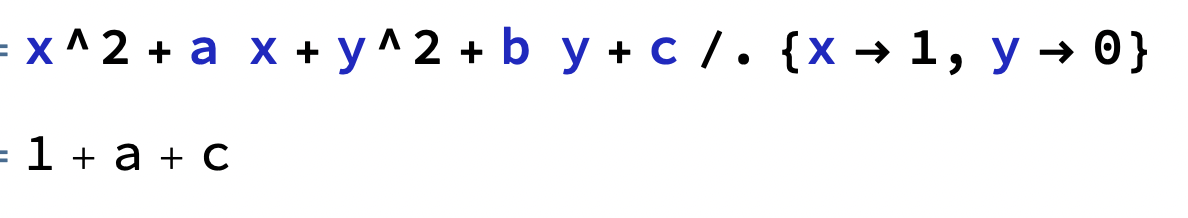
Trinity2 skrev:Hur?
du har rätt. jag läste fel. (har korrigerat inläggen)
Läxhjälp skrev:den andra ekvationen i linjära ekvationerna ska korrigeras.
såg att jag räknade fel, det ska stå 2b + c = -4
Yousefyxa skrev:Detta är uppgiften
Jag har lyckats lösa första delen av uppgiften med minsta kvadrat metoden, här är min lösning:
ser det bra ut? och min fråga är hur gör jag för att hitta cirkelns radie och medelpunkt?
Löser du (rättat) ekv.sys får du
{a,b,c}={-9/5, -23/10, 2/5}
Cirkeln ges av
2/5 - (9 x)/5 + x^2 - (23 y)/10 + y^2 = 0

Nästa steg är att kvadratkomplettera VL;
(x - 9/10)^2 + (y - 23/20)^2 = (9/10)^2 + (23/20)^2 - 2/5
vilket ger
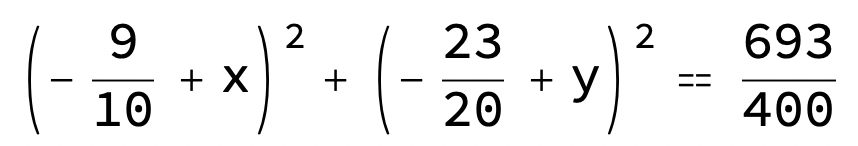
Nu vet du centrum och radie.
Trinity2 skrev:Yousefyxa skrev:Detta är uppgiften
Jag har lyckats lösa första delen av uppgiften med minsta kvadrat metoden, här är min lösning:
ser det bra ut? och min fråga är hur gör jag för att hitta cirkelns radie och medelpunkt?
Löser du (rättat) ekv.sys får du
{a,b,c}={-9/5, -23/10, 2/5}
Cirkeln ges av
2/5 - (9 x)/5 + x^2 - (23 y)/10 + y^2 = 0
Nästa steg är att kvadratkomplettera VL;
(x - 9/10)^2 + (y - 23/20)^2 = (9/10)^2 + (23/20)^2 - 2/5
vilket ger
Nu vet du centrum och radie.
så cirkelns radie är ?
och centrum är (x , y)= (9/10 , 23/20)? tänker jag rätt nu?
Ja
Så här blir det, med röd streckad = cirkel från kvadrakompl. ekvation

Radien kan skrivas