Cirkel som tangerar en rät linje


Såhär började jag lösa uppgiften, men kom inte så mycket längre. Någon som har tips på hur jag ska gå vidare? Tack på förhand!
Här är en liten skiss av situationen:
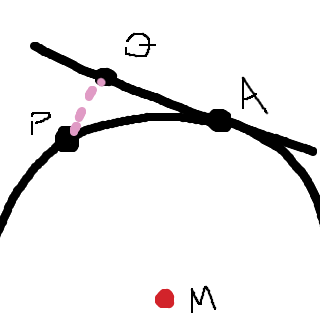
Vilka sträckor finns mellan dessa punkter, och vilka längder har de?
Likbent triangel med sidorna AP, r och r. Inget som poppar upp i mitt huvud av det hehe.
Tangenten, har den nån ekvation?
Cirkeln har också en ekvation
Linjen qp har en riktningskoeff som hänger ihop med tangentens riktning
Cirkelns derivata i tangeringspunkten har en relation till tangentens riktning
Inga punkter är fixa så vi kan lägga ett koordinatsystem var vi vill
Kan ovanstående ge någon ide till lösning?
(obs: jag har inte löst uppgiften, bara funderat lite på hur jag skulle angripa problemet)
@Ture: Intressant metod! Min tanke var följande (men din metod kan nog vara mer effektiv): Vi får en rätvinklig triangel om vi drar sträckan AP. Längden av AP är 5 pga. Pythagoras sats, och då har vi följande situation:
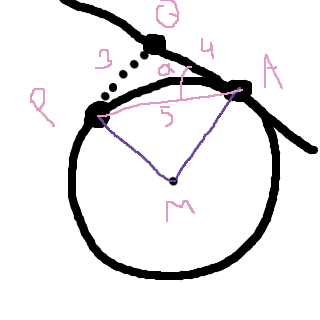
Vinkeln MAQ är 90 grader eftersom linjen är en tangent till cirkeln, och då kan vi beräkna storleken hos vinkeln alfa. Därefter kan vi använda trigonometri för att hitta r. :)
@Ture tangentens ekvation är
linjen qp har ekvationen
cirkelns derivata i tangeringspunkten är samma som tangentens derivata
Får inga idéer till lösning av det här, får du det?
Radien är vinkelrät vid tangenten i punkten A. Enligt smutstvätt kan man beräkna vinkeln alfa. Därmed vet man vinklarna i basen i P och A. Därmed är det nästan klart.
Jag vet inte om arcusfunktionerna ingår i Matte 4.
Med beteckningar enl. Smutstvätt:s figur får man snabbt att
.
Med cosinussatsen är det sedan relativt smärtfritt att bestämma radien r.
Varför cosinussatsen? Vi kan ta fram att vinkeln alfa är , dvs. vinkeln MAP är , och sinus av den vinkeln, multiplicerat med fem, är vår radie r. Om ett svar i decimalform ska tas fram blir det kanske värre dock? Eller vänta nej, det går väl också att beräkna?
Absolut en god lösning Smutstvätt - men återigen kommer vi inte ifrån arcusfunktioner.
Ska vi ta fram radien exakt finns väl ingen annan möjlighet.
Nej, det är sant. Arcusfunktionerna ingår i Ma4, så det är nog lugnt, även om det kanske krävs lite pill för att få till . :)
På det här provet är det inte tillåtet med räknare, så svårt att räkna ut arcsin
Trigonometri behövs inte:

Eller i och för sig behöver man aldrig veta vad arcsin av den vinkeln är.
Rätt svar ska vara 25/6
Du behöver ingen trigonometri. Notera den rätvinkliga triangeln som uppstår i bilden jag skickade. Där kan du ställa upp Pythagoras sats.
Här följer en lösning som inte utnyttjar någon trigonometri:
Situationen ser ut så här. Pythagoras sats ger enkelt att . Kallar vi vinklarna och för respektive inses att , eftersom radien är vinkelrät mot tangenten. Då triangeln är likbent följer att även . Triangelns vinkelsumma ger då .

En likbent triangel kan med en bisektris delas upp i två rätvinkliga trianglar där basen delas mitt itu vid punkten , det vill säga att (att bevisa detta är inte så svårt, så jag överlämnar det åt läsaren). I detta fall ger det två rätvinkliga trianglar, som är likformiga med triangeln !

Detta låter oss med likformighet bestämma radien.

Vi får med likformighet:
ur vilket vi enkelt löser ut att .
Om vi lägger cirkeln medelpunkt i Origo och punkten A på x-axeln så gäller följande:
A har koordinaterna (r,0)
Q har koordinaterna (r,4)
P har koordinaterna (r-3,4)
Använder vi avståndsformeln för punkten P till origo får vi
r2 =(r-3)2 + 42
r2 = r2 +9 -6r +16 som efter förenkling blir
6r = 25
r = 25/6
Ursäkta, jag ser nu att jag utgått från specialfallet då AMP är rät, annars behövs liter mer trig. Men Alvins lösning är snygg!
Smutstvätt skrev:Ursäkta, jag ser nu att jag utgått från specialfallet då AMP är rät, annars behövs liter mer trig. Men Alvins lösning är snygg!
Skafts lösning är snyggare! :-)
Tack så mycket allihopa för hjälpen!








