Centripetalkraft
Hej!
Jag pluggar till mitt fysikprov, och fastar på uppgift 154 i impuls 2 boken. Uppgiften lyder "På Tom Tits Experiment i Södertälje finns en horisontell cylinder som man kan gå in i. Cylindern sätts sedan i rotation. Därefter sänks golvet i cylindern och besökarna hänger då fast mot väggen. Rita in de tre krafter som verkar på personen på bilden. Om två krafter är lika stora så rita dem med lika långa pilar.".
Krafterna som verkar på personen förstår jag är tyngdkraften nedåt, normalkraften och en friktionskraft. Varför blir friktionskraften uppåtriktad och lika stor som tyngdkraften? Jag försår att Fr måste vara 0 i y-led för att inte personen ska falla ned - men varför kan inte det vara normalkraften som går upp?
Likaså, varför blir normalkraften vår centripetalkraft? Beror det på att normalkraften alltid har fäste vinkelrätt mot väggen/underlaget/människan och då blir riktad mot cirkelns centrum? Isåfall, blir då en kraft som går inåt i en cirkulär rörelse alltid en centripetalkraft, eller kan det finnas både en enskild normalkraft och en enskild centripetalkraft samtidigt i snurran? Tack på förhand :)

Det stämmer nog att centripetalkraften och normalkraften blir samma här. Mer korrekt är antagligen att normalkraften är lika stor som centrifugalkraften. Men egentligen bör man nog inte prata om normalkraft i detta fallet eftersom det är en roterande rörelse.
Okej. Jag förstår fortfarande inte helt. Så det stämmer att han påverkas av en lika stor tyngdkraft och friktionskraft i y-led, så att resultanten=0? Går friktionskraften upp då eftersom att den är motsatt riktad att personen glider nedåt?
Kan man uttrycka sig som följande, eller är detta inkorrekt?: Personen påverkas av en centrifugalkraft utåẗ. Då det är en cirkulär rörelse blir normalkraften inåt riktad och större än centrifugalkraften, vilket skapar en resulterande kraft=centripetalkraften.
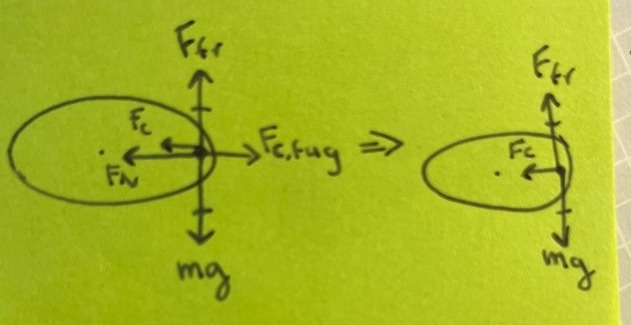
Lokalt är din figur till vänster korrekt. Centrifugalkraften är en upplevd kraft av personen i snurran. För en observatör utifrån gäller figuren till höger. Då kan man bortse från centrifugalkraften. Friktionskraften är lika stor som gravitationskraften som du skriver.



