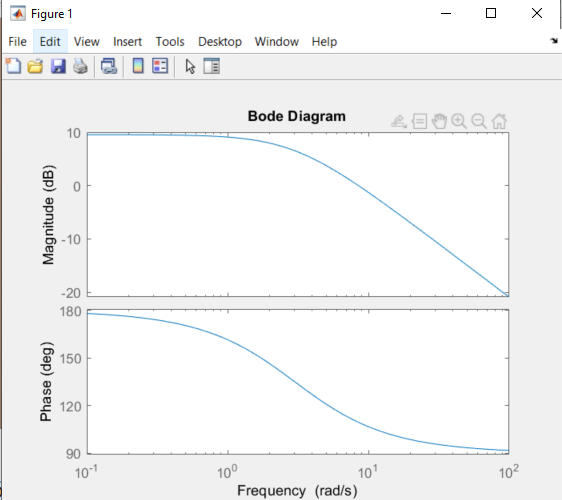
Bodediagram - hur hittar man lutning
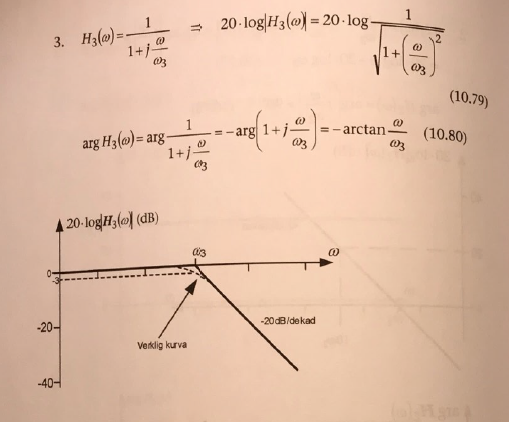
Lite osäker hur man räknar ut lutningen. Vet att om överföringsfunktionen istället är H(ω)=jωω2 så är lutningen 20-010ω2-ω2, men får inte till det till denna (bild).
För låga frekvenser så är K=-3
Brytfrekvensen är ω3
G(s)=-3(1+sω3)
Vilket ger ungefär följande fas - & amplitudskruvor:
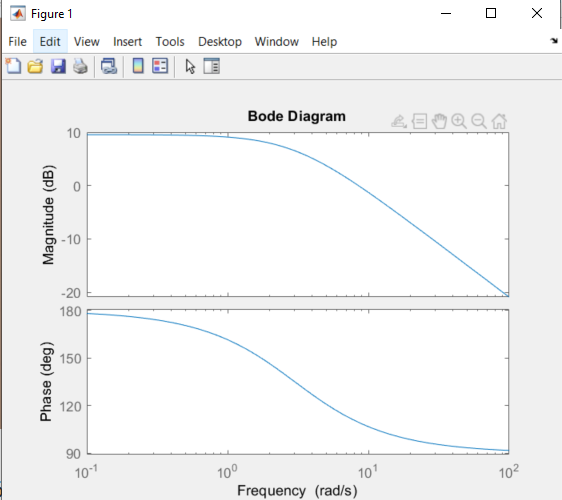
Nu har jag satt ett värde för ω3, nämligen ω3=3
Tillägg: 13 nov 2022 13:33
Oj, skalan var i decibel!
Det ska egentligen vara K≈0.71.
Cien skrev:
Lite osäker hur man räknar ut lutningen.
En lutning på 20 dB/dekad (eller 6 dB/oktav) betyder alltså en faktor 10 i spänning per dekad, en faktor 100 i effekt.
Dracaena skrev:För låga frekvenser så är K=-3
Brytfrekvensen är ω3
G(s)=-3(1+sω3)
Vilket ger ungefär följande fas - & amplitudskruvor:
Nu har jag satt ett värde för ω3, nämligen ω3=3
Tillägg: 13 nov 2022 13:33
Oj, skalan var i decibel!
Det ska egentligen vara K≈0.71.
Tack ska du ha. Men om man ska rita för hand så förhåller man sig till räta linjer om jag har förstått rätt? Om lutningen är k, låt oss kalla ω=x samt 20log|H3(ω)|=y är då k=ΔyΔx=-20-010ω3-ω3?
Tillägg: 14 nov 2022 14:50
Vad jag försöker komma till bukt med är hur jag kan framställa att lutningen är -20dB/dekad