Blir svaret 20m ?

Är du säker på att y=0,8 om x=0?

Tror det, om jag utgår från de jag räknat fram så liksom, ja.. 
För om hon fångar bollen vid 0,80m höjd.. liksom.. visst kan hon stå 0m från bollen om någon bara har kastat upp bollen rätt upp i luften & hon fångar den liksom så.. men.. Nu blir jag osäker.. vet inte om det är 0m eller 20m.. men på bilden så ser de ut så här, så antar att det är 20m

Testa att stoppa in x=0 i funktionen du fått. Blir y=0.8?

Tillägg: 25 jul 2024 12:27

Dessutom ska du aldrig lita på bilder. Avståndet kan likväl vara 2cm som 20000km.

Hej,
 
Jag stoppa in x=0 i y=-0,10x^2 + 2x+1  & testa även med x=20
och inget av de x värden gav mig ett y värde som är 0,80

Vad betyder det? att jag fått fram fel x värden dvs räknat fel eller att jag tänkt fel med hur jag löser uppgiften? 

Min tanke 
Jag har: y=-0,10x^2 + 2x + 1 
y=  0,80

0,80=-0,10x^2 + 2x + 1 
& så räknar jag fram x värdet liksom? med hjälp av pq.
Det x värde som jag får fram är svaret på uppgiften..?

Helt rätt tänkt, men ditt svar blir fel eftersom att de inte uppfyller ekvationen.

Gör om och visa dina beräkningar här.

Jag räkna om allt men får ut samma svar? 

Om det står 0=”uttryck” så kan du bara byta plats direkt så att det blir ”uttryck”=0. 

Avrunda roten ur 102 till 10,1 istället.

Jag använde räknare när jag stoppa in de olika x värdena jag fick fram när jag tog 10,1
& fick fram att både ett x= -0,10 och ett x=20,1 blir ger ett y=0,799 

****

visar:

Eftersom att hon inte kan stå -0,10 m från utslagspunkten (det är ju -, det går väl inte?) så antar jag att när bollen är 0,80m över marken befinner hon sig 20,10m från utslagsplatsen dvs x=20,1 är liksom svaret? Det är exakt 

***
Fråga: Valde du att avrunda roten ur 102 till 10,10 istället för 10, för att svaret till 
(roten ur) 102 = 10,099 ... så =10,1 är liksom säkrare än bara 10?

Det är förmodligen meningen att du ska svara 10,1, men jag tycker det är en dålig uppgift, för talen 2 (framför x) och 1 i funktionen har bara en siffras noggrannhet.

-0,1 kan hon väl stå på, men bollen är aldrig där. Den lösningen motsvarar negativ tid, alltså att bollen kom farande och passerade det som är utslagspunkten vid tiden 0.

Svaret 20,1 är inte exakt, det är motsatsen till exakt. Det är ungefärligt, avrundat. Om vi antar att de givna talen är exakta (vilket är orimligt för en fysikalisk situation) så är det exakta svaret $10+\sqrt{102}$.

Tack. Men exakt menar jag MER exakt än mitt första svar på 20, men jag skriver nog bara båda med förklaring. 
dvs: 
Avrundat svar: 20,10m 
Exakt svar: x=10 + (roten ur)102

Har du något facit till frågan? Jag är lite nyfiken på vilket svar de söker.

Jag skicka min uträkning till läraren & mina svar. Fråga läraren om svaren och väntar på ett svar. Lovar att komma tillbaka hit och skriva det läraren säger om det hela sen. 

Du skall lösa ekvationen 0,8 = -0,10x²+2x+1, d v s -0,10x²+2x+0,2 = 0 eller x²-20x-2= 0.

Som du ser är x-koordinaterna för skärningen mellan den blå och den gröna kurvan somma som för skärningaarna mellan den lila kurvan och y-axeln. Omskrivningen gjore jag för att kunna anänvda pq-formeln, som ju kräver att koefficienten för kvadrattermen är "osynlig etta". Lösningen blir $x=10\pm \sqrt{102}$, där den negativa roten saknar fysikalisk betydelse. Frågan är väl om svaret skall avrundas till 20 eller 20,1 m, och jag skulle rösta på 20 m. Vi har inte tre siffrors noggrannhet på indata, så vi borde inte ha det på svaret heller.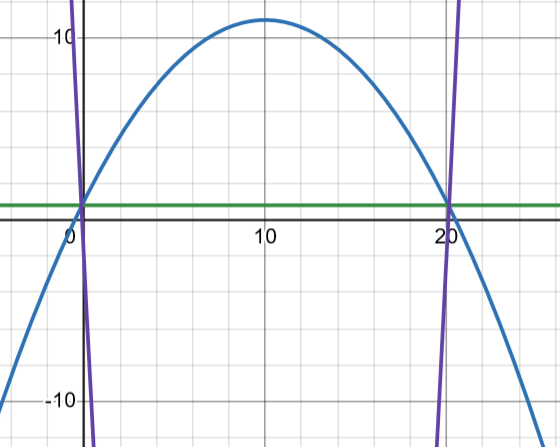

Hej igen,

Till den som fortfarande undrar så sa läraren att "Både 20 eller 20,1 är acceptabelt". 

Det är inte en acceptabel lösning på uppgiften, men för förståelsen av den kan tilläggas
att svaret 20 m går att få med huvudräkning.

1:an i funktionsuttrycket står för bollens höjd över marken vid utslaget.
Bollen fångas på 0,8 m höjd.
Talen 1 och 0,8 kommer att ha liten inverkan på svaret.
Om vi bortser från dem får vi

-0,1x² + 2x = 0
x(2 - 0,1x) = 0
x₁=0
x₂=20