Bisektris

Uppgiften lyder "I en triangel är en vinkel 120. Bisektrisen till denna vinkeln delar motstående sida i två delar med längderna 1cm respektive 2cm. Beräkna triangelns area."

Här är en visualisering.

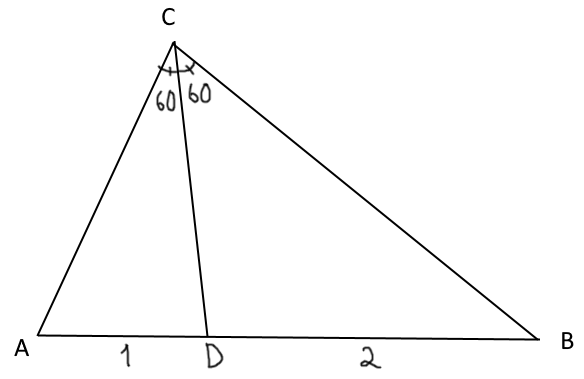
Formeln för arean är ju $\frac{AC\times BC\times \sin \left(120\right)}{2}$

Man kan inte använda bisektrissatsen då vi saknar 2 av längderna. $(\frac{AD}{BD}=\frac{AC}{BC}) \to Saknar BC och AC$

Jag testa att använda mig av cosinussatsen vilket gav mig 3 ekvationer, 1 för varje triangel:

$$\begin{gathered} ADC \to 1^2=A{C}^2+C{D}^2-2\times AC\times CD\times \cos \left(60\right) \\ BCD \to 2^2=B{C}^2+C{D}^2-2\times BC\times CD\times \cos \left(60\right) \\ ABC \to 3^2=A{C}^2+B{C}^2-2\times AC\times BC\times \cos \left(120\right) \end{gathered}$$

Här går det tekniskt sett att lösa ut de olika längderna men det känns lite för jobbigt att lösa när man inte har en miniräknare.

Det tredje sättet jag testa var med sinussatsen.

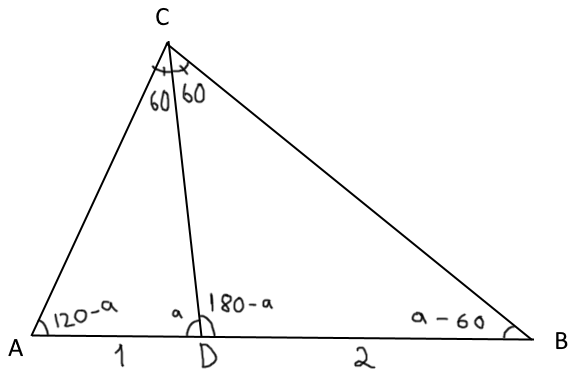
Då satt jag in lite vinklar i triangeln vilket bilden visar.

Mha sinussatsen får jag 2 ekvationer:

$$\begin{gathered} BCD\to \frac{\sin \left(60\right)}{2}=\frac{\sin (180-a)}{BC} \\ ACD\to \frac{\sin \left(60\right)}{1}=\frac{\sin (120-a)}{AC} \end{gathered}$$

2 ekvationer för att lösa ut 3 variabler går inte.

Är det något steg jag missar eller finns det något annat jag kan göra för att lösa uppgiften? Eller är det kanske så att jag bara ska försöka lösa ekvationssystemet jag fick genom cosinussatsen?

Facit säger $\frac{9\sqrt{3}}{14}c{m}^2$