Bil i loop
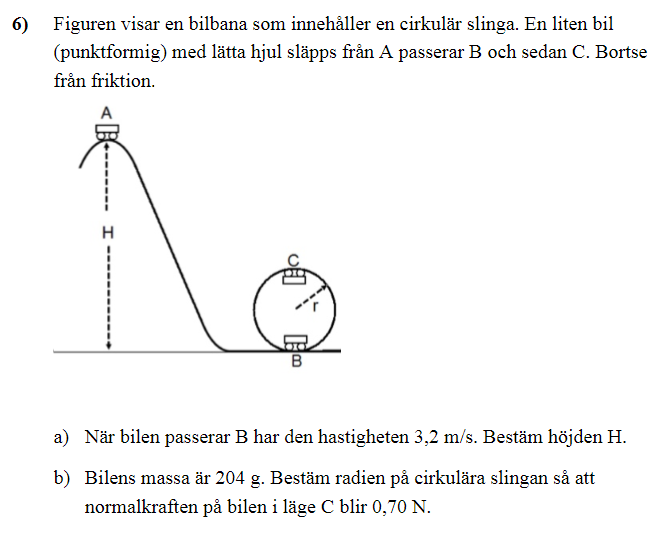Hej, jag skulle upskatta hjälp med denna uppgift. jag har löst uppgift a) och fick fram till att höjden H är 0.52m vilket enligt facit är rätt. Men nu har jag fastnat på fråga b). Detta har jag gjort hittilts men har ingen aning hur jag ska fortsätta.
(Förlåt för handstilen)
Edit: Vet inte ens om det jag har börjat med är rätt. Tänkte bara att Fc = mv^2/r och att jag skulle behöva räkna ut vad v blev först.
Hej Ubow!
Du har delvist börjat rätt.
När bilen befinner sig i loopen så åker den i en cirkulär bana. För att kunna göra så behövs det en centripetalkraft. Det är normalkraften från loopens bana som hela tiden utgör denna centripetalkraft. För normalkraften är ju alltid riktad vinkelrätt ut från banan och in mitt loopens mitt, precis som centripetalkraft!
Ju snabbare bilen åker, desto större centripetalacceleration som behövs. Ju snabbare bilen åker längs loopen, desto snabbare "trycker" den mot banan vilket ger upphov till större normalkraft.
När den befinner sig i läge C är det tre krafter som verkar på bilen: normalkraft från banan riktad nedåt, bilens tyngdkraft riktad nedåt, och bilen som "trycker mot banan".
För att bilen precis ska klara av att passera punkt C krävs att bilen har en hastighet v så att tyngdaccelerationen är lika stor som centripetalaccelerationen. Om den åker snabbare än v så ger det upphov till en normalkraft.
Om man summerar krafterna i Y-led så får man:
mac - mg = N (1)
där c avser centripetalacceleration.
ac = v2/r där v är hastigheten i punkt C. Hastigheten i punkt B är känd, det som återstår att räkna ut är alltså vilken radie loopen har så att bilen får just den hastigheten i punkt C så att ekvation (1) uppfylls. För att göra så behöver man relatera kinetisk energi med potentiell energi, som du så fint redan har börjat med :)
Hoppas det här var till någon hjälp!
Truppeduppe skrev:Hej Ubow!
Du har delvist börjat rätt.
När bilen befinner sig i loopen så åker den i en cirkulär bana. För att kunna göra så behövs det en centripetalkraft. Det är normalkraften från loopens bana som hela tiden utgör denna centripetalkraft. För normalkraften är ju alltid riktad vinkelrätt ut från banan och in mitt loopens mitt, precis som centripetalkraft!
Ju snabbare bilen åker, desto större centripetalacceleration som behövs. Ju snabbare bilen åker längs loopen, desto snabbare "trycker" den mot banan vilket ger upphov till större normalkraft.
När den befinner sig i läge C är det tre krafter som verkar på bilen: normalkraft från banan riktad nedåt, bilens tyngdkraft riktad nedåt, och bilen som "trycker mot banan".
För att bilen precis ska klara av att passera punkt C krävs att bilen har en hastighet v så att tyngdaccelerationen är lika stor som centripetalaccelerationen. Om den åker snabbare än v så ger det upphov till en normalkraft.
Om man summerar krafterna i Y-led så får man:
mac - mg = N (1)
där c avser centripetalacceleration.
ac = v2/r där v är hastigheten i punkt C. Hastigheten i punkt B är känd, det som återstår att räkna ut är alltså vilken radie loopen har så att bilen får just den hastigheten i punkt C så att ekvation (1) uppfylls. För att göra så behöver man relatera kinetisk energi med potentiell energi, som du så fint redan har börjat med :)
Hoppas det här var till någon hjälp!
Hej! tack för svaret!
Tror jag fattar en del av det du har skrivit. Undrar bara om "mac - mg = N (1) " är samma sak som Fc-Fg=FN där Fc är centripetal kraften, Fg är tyngkraften och FN normalkraften. Ska jag då byta ut Fc mot mv^2/r och sedan räkna ut vad v är med hjälp av formeln jag fick fram? För jag vet redan vad Fg och FN är.
Börjar bli sent, så tror jag försöker att fortsätta med uppgiften imorgon. Markerar det som klart då. Tack på förhand!!
Tillägg: 23 okt 2024 06:54
Förlåt, menade beräkna radien, inte v.
