Bevisa konvergens mot 0

Hej, jag har svårigheter med följande två uppgifter: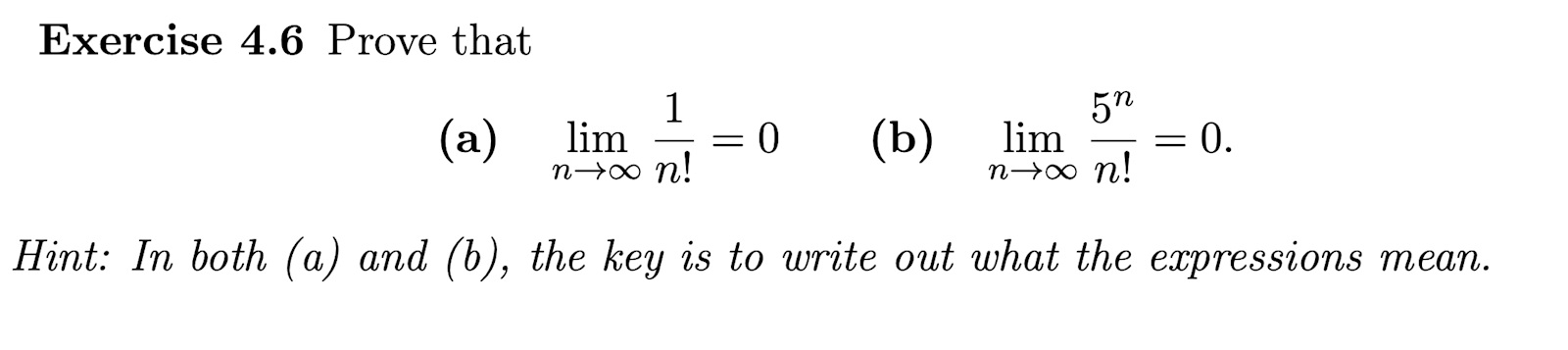

Om vi börjar med a. Jag vill hitta ett n > N så at a_n<ε. Då kan jag lösa ut n! > 1 / $ε$ . Men hur gör jag nu. Jag kan väl inte ersätta n! med n i och med att n är mindre eller lika med n! ??

Om du inte måste använda typ epsilon delta så kanske man kan resonera på följande sätt:

$n! = n \cdot (n-1) \cdot (n-2)...3 \cdot 2 \cdot 1$

$n! > n(n-1)$

$\dfrac{1}{n} \cdot \dfrac{1}{n-1}$ blir en produkt av två bråk som uppenbarligen går mot 0, varav produkten går mot 0.

Men notera att $\dfrac{1}{n!} <>$ .

Så om $\dfrac{1}{n(n-1)} \rightarrow 0$ då $n \rightarrow \infty$ måste det betyda att samma måste gälla för $\dfrac{1}{n!}$ .

Tack, jag ska klura vidare på detta.

Svara