Bevisa cosinus additionsats

Jag har försökt att rita upp vinklarna men allt jag ser att använda är trig 1:an som jag inte tror det är meningen att använda.

Visa spoiler
Man ska använda sig av cosinusatsen och av avståndsformeln
Använd avståndsformeln mellan u och v.
Använd avståndsformeln mellan u-v och där vinkeln är 0.
Dessa ger samma avstånd och kan därför sättas lika med varandra.
Mrpotatohead skrev:Använd avståndsformeln mellan u och v.
Använd avståndsformeln mellan u-v och där vinkeln är 0.
Dessa ger samma avstånd och kan därför sättas lika med varandra.
Vilken koordinat för u och v är det jag mäter?
Avståndet mellan (cos(u), sin(u)) och (cos(v), sin(v)).
Mrpotatohead skrev:Avståndet mellan (cos(u), sin(u)) och (cos(v), sin(v)).
Är det inte samma avstånd som för bara sin(u) och sin(v)?
Varför vill man ha de avstånden?
Det är två punkter på enhetscirkeln. Förstår inte riktigt vad du menar.
Mrpotatohead skrev:Det är två punkter på enhetscirkeln. Förstår inte riktigt vad du menar.
Det är jag som inte fattar, förstår jag rätt om vi då mäter avståndet från dessa punkter:

Mrpotatohead skrev:
Okej so far soo good, men varför är det avståndet viktigt?
För att det är samma avstånd som mellan punkten där vinkeln är u-v och där cirkeln skär x-axeln till höger!
Mrpotatohead skrev:För att det är samma avstånd som mellan punkten där vinkeln är u-v och där cirkeln skär x-axeln till höger!
Men hur kan vi ens veta att vinkel u är i 2:a kvadranten?
Det spelar ingen roll. Du kan sätta den var du vill.
Mrpotatohead skrev:För att det är samma avstånd som mellan punkten där vinkeln är u-v och där cirkeln skär x-axeln till höger!
Det här förstår jag inte riktigt
Man kan tyvärr inte se din bild Jan Ragnar så jag fixade en egen. 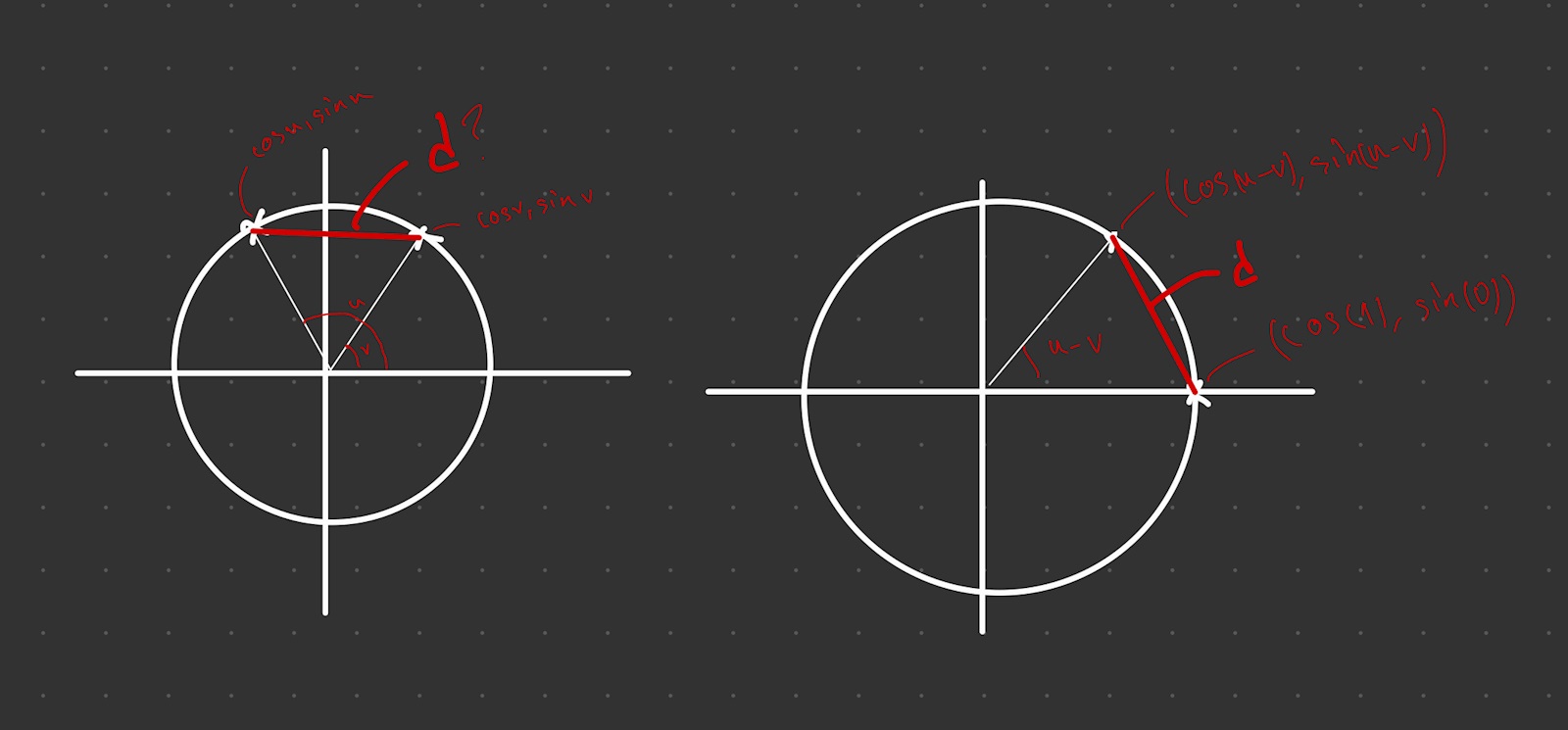
Efter omdöpning av filen borde det nog synas bättre.
.jpg?width=800&upscale=false)


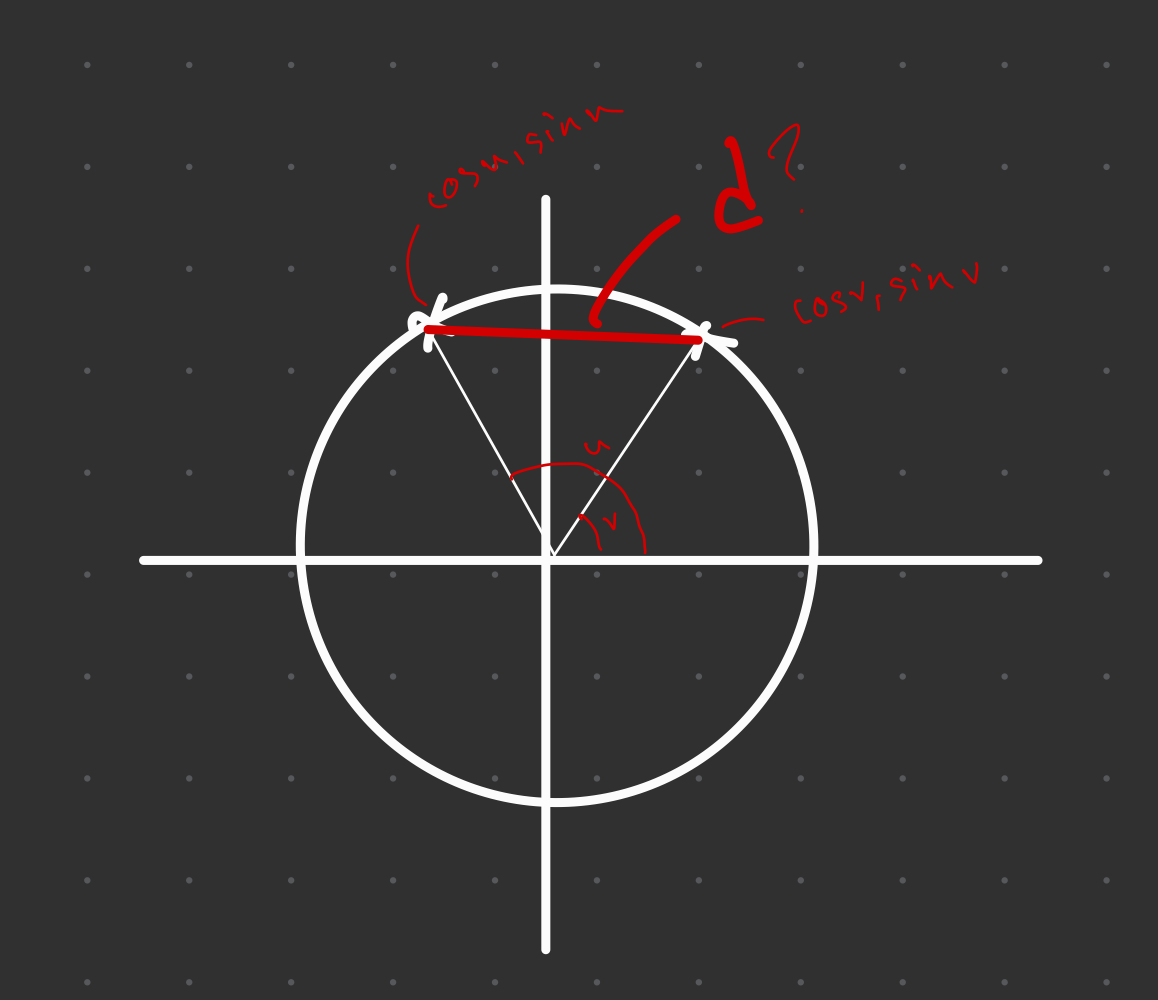
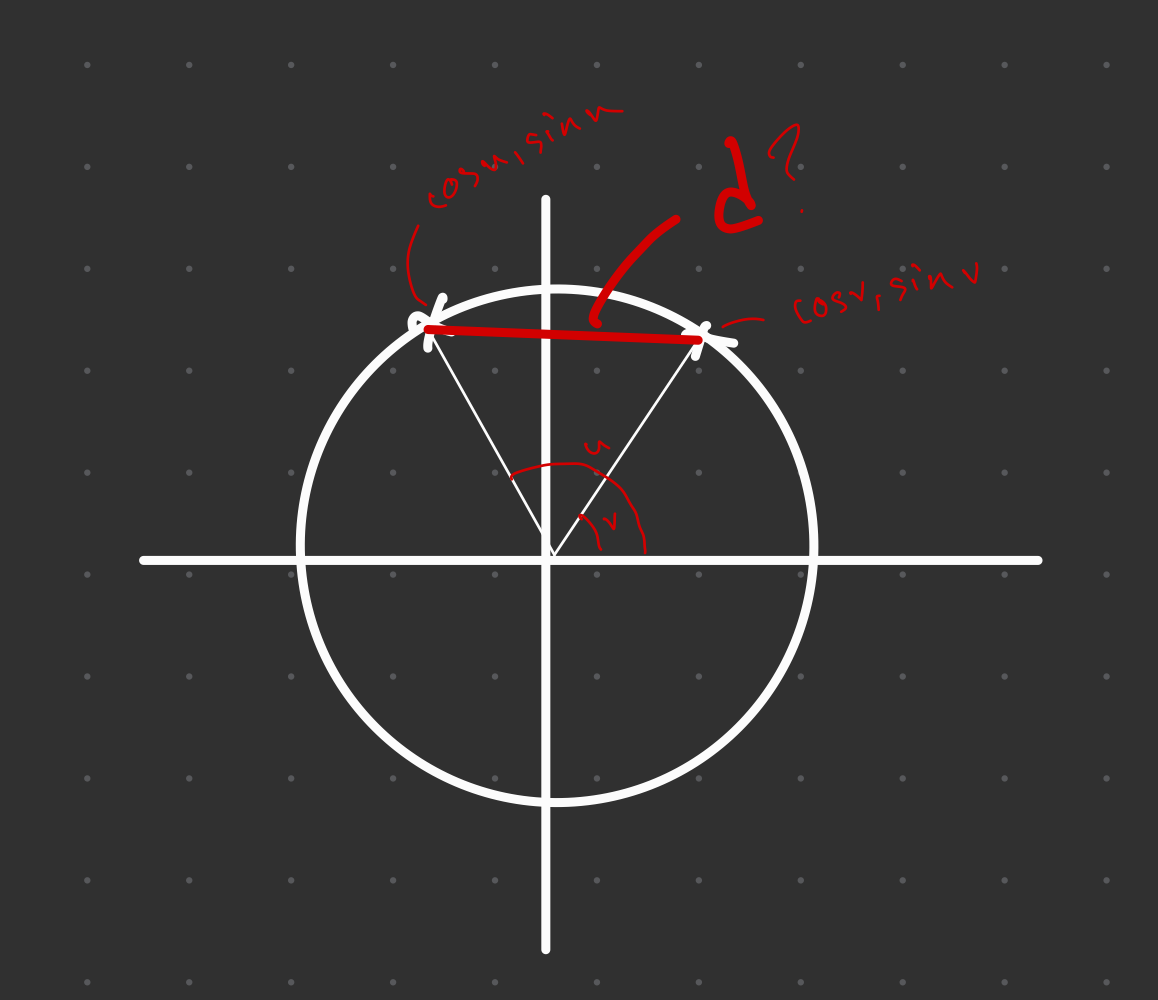

.jpg?width=800&upscale=false)
