Bevisa att det inte är lika med 2.

Motsägelsebevis?

Antag att a²-4b=2

Jag håller med MaKe om att du skulle kunna försöka dig på ett motsägelsebevis.

Det finns säkert många sätt man kan göra det på, men här är en strategi som du kan prova:

Jo,

a^2 -4b = 2

b = (a^2-2/4)

så b är samma som a^2-2/4

...

så om det ska vara 2 måste a^2-2 vara dividerbart med 4?

a(a)-2

om a är jämnt är det 2a

Då blir det 4a^2-2 som.. inte kan divideras med 4? För.. Jag vet inte.

Om det är udda blir det (2a+1)(2a+1) = 4a^2+4a+1

Vi har att $a^2 - 4b = 2$
Men 4b är jämnt, 2 är jämnt
Vi har alltså $a^2$ - ett jämnt tal = jämnt tal
Vad säger det då om $a^2$ och i sin tur, $a$?

Jag vet faktiskt inte

$a^2 -4b = 2$
$a^2 = 2+4b$
$a^2 = 2(1+2b)$

Om a^2 blir ett jämnt tal så måste a också vara ett jämnt tal.

Dkcre skrev:

Om a^2 blir ett jämnt tal så måste a också vara ett jämnt tal.

Precis! Testa att sätta $a=2k$ och se vart det leder. 

4k^2 -4b = 2

Och då kan det här inte bli 2?

Ja. Varför är det så?

Jag vet inte Alex, jag är ledsen men jag kan inte svara på det. Förstår inte.

Okej, om vi förenklar uttrycket såhär:
$4k^2 - 4b = 2$
$4(k^2 - b) = 2$
$2(k^2 - b)= 1$
Är detta möjligt? 

Ett kvadrerat tal subtraherat med ett annat tal ska bli = 0.5

Jag ser inga direkta problem med det egentligen?

Om K = sqrt(0.75) och b är 0.25 blir det 0.5.

¤¤¤¤¤¤¤¤¤¤¤

Ah, jaha, jag läste nu. Hur kom vi fram till det då. Ska kolla. Eller jaha, det framgår i själva frågan till att börja med XD

Nej, då ser det inte ut att vara möjligt faktiskt :)

¤¤¤¤¤¤¤¤¤¤¤

Tack du..

Lägg märke till det lite subtila men väldigt användbara tricket AlexMu använde här:

Om $a$ är ett heltal och $a^2$ är delbart med ett primal $q$ (i detta fallet: 2), så måste även $a$ vara delbart med $q$, och alltså är $a^2$ delbart med $q^2$. 

Hänger du med på varför detta är sant? ^_^

Nej oggi, faktiskt inte. Det är lite svårt för mig att hänga med rent allmänt :P

oggih skrev:

Lägg märke till det lite subtila men väldigt användbara tricket AlexMu använde här:

Om $a$ är ett heltal och $a^2$ är delbart med ett primal $q$ (i detta fallet: 2), så måste även $a$ vara delbart med $q$, och alltså är $a^2$ delbart med $q^2$. 

Hänger du med på varför detta är sant? ^_^

Är lite piggare i huvudet idag så kanske förstår.

Försöker mitt yttersta för att hänga med, men ser ingen logik rakt av i det du skriver. Det kan jag inte..

Om jag gör det till någonting mer konkret då.

6 & 6^2, dvs 6 & 36. Primtal.. säg 3.

36/3 = 3.

¤¤¤¤¤

Det är delbart för 3 eftersom talet 36 innehåller faktorn 3.

Om 36 innehåller faktorn 3, måste 6 också vara delbart med 3. Varför det då..

¤¤¤¤¤

För att $\sqrt{36} = 6$, dvs 6x6 = 36.

..

Nej, jag kan inte.

¤¤¤¤¤

Typ att en faktor kan inte bara dyka upp sådär utan måste ha funnits hela tiden om det kvadrerade talet enbart har blivit kvadrerat från ett annat tal och ingen annan operation har vart inblandad, då. Men mer varför än så kan jag inte förklara.

a^2 är delbart med q endast om a^2 innehåller faktorn q.

om a^2 innehåller faktorn q måste a det också, eftersom ett tal multiplicerat från andra tal består av olika faktorer, det är lite fundamentalt för hela grejen.

Men då.. nej, om q är typ hälften av a^2 då, då kan inte a delas med q igen..

¤¤¤¤

Det kräver för mycket brain power, jag kan inte förstå det utifrån att resonera själv.

En egenskap som primtal har är att vi inte kan multiplicera ihop två tal för att få ett primtal. När vi kvadrerar ett tal är det exakt vad vi gör, vi multiplicerar ihop tal.
Nya delare till kvadraten kvadraten kommer dyka upp, men eftersom vi inte kan multiplicera ihop tal för att få primtal är det omöjligt att någon av de nya delarna är ett primtal.

Lite mer invecklad förklaring

Jag vet inte om man går igenom detta i bevisdelen i matte 4 men en fundamental egenskap av heltalen är förmågan att faktorisera dem till primtal, så kallad primtalsfaktorisering. Om ett tal inte är ett primtal är det per definition en produkt av andra tal, som i sin tur kanske är primtal eller sammansatta. Om de är sammansatta kan vi fortsätta dela upp dem till faktorer av primtal.

Vi tar exemplet $12$. Vi kanske först ser att $12 = 3 \cdot 4$. 3 är primtal så vi lämnar det där, men $4=2\cdot 2$ och 2 är primtal. Då får vi att $12 = 2\cdot 2 \cdot 3$ och nu har vi hittat primtalsfaktoriseringen av $12$. 

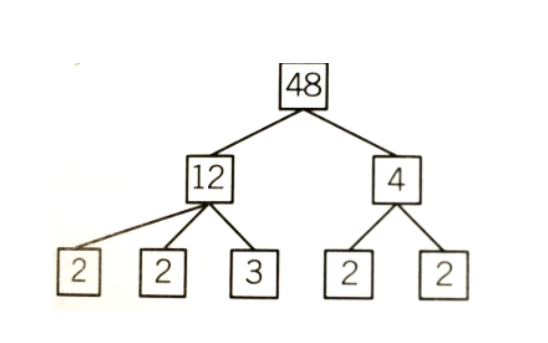Primtalsfaktorisering av 48

När vi kvaderar $12$ kan vi lika gärna bara kvadrera primtalsfaktorerna. Alltså
$12^2 = 2^2 \cdot 2^2 \cdot 3^2 = 2^4 \cdot 3^2$. Om $12^2$ är delbart med något tal måste det vara delbart någon av primtalsfaktorerna eftersom de representerar exakt samma tal. 
På så sätt kan vi exempelvis se att $12^2$ är delbar med $3^2$ eftersom det är något som går jämnt i primtalsfaktoriseringen. $3 \cdot 2^3$ är också delbar av samma anledning. Men $3^3$ är inte det eftersom vi inte har tillräckligt med treor i talet. 

Det är omöjlgt att nya primtal dyker upp i kvadreringen av ett tal. Den enda skillnaden är att i kvadraten så har gamla primtal i faktoriseringen en högre exponent. Det kan inte dyka upp nya 

Tack för förklaringen Alex. Läste igenom det.

Men jag fattar inte riktigt ändå. Kommer nog ta mig ett tag.

Får gå tillbaka och läsa det sen igen.

a²-4b = 2   (a och b heltal)

1. Om ett tal minus ett jämnt tal är ett jämnt tal måste talet vara jämnt.

2. Om a² är jämnt, måste a vara jämnt och a² delbart med 4.
      (Om a*a innehåller faktorn 2 måste den finnas i a och därmed finns en faktor 2 i vardera a:et)

3. Då är vänsterledet delbart med 4 (du kan bryta ut 4).

4. Men högerledet är inte delbart med 4, alltså är a²-4b = 2 en motsägelse.

Hur långt är du med?

Jag är med på uppgiften hyfsat i alla fall, men det är väldigt svårt.

Det är bara dom logiska deduceringarna som är besvärliga. Om P är Q och Q är R, måste P vara R och Q^2 måste då vara etc.

Jag har svårt för att hänga med, kan inte hålla i tråden när jag tänker på det. Vet inte vad jag ska säga.

Det är mest det oggi la fram där som jag inte är med på nu, och Alex förklaring. Orkar inte mentalt hänga med i resonemanget.

@@@@@

Eventuellt att jag genomför extremt många uppgifter av logisk natur på väldigt grundlig nivå (ännu mer grundligt :p) så kanske jag blir lite bättre.

Jag delade upp motsägelsebeviset i fyra steg och undrade hur långt du är med.

Är du med på 1.?

Nej inte riktigt, ett tal minus ett jämnt tal borde kunna vara vilket som helst. Räknar jag på det så ser jag ju att det inte stämmer dock.

Ska fundera och ge ett svar sen. Julbord nu.

Ok, hoppas det smakar!

Sedan kan du skriva om a²-4b = 2
som a² = 2 + 4b.

Båda termerna i högerledet är jämna. Är du med på att summan a² då måste vara jämn?

Tillägg: 14 dec 2024 19:07

ett tal minus ett jämnt tal borde kunna vara vilket som helst

Frågan gällde om ett tal minus ett jämnt tal blir ett jämnt tal,
vad gäller då om det första talet?

Louis skrev:

Ok, hoppas det smakar!

Sedan kan du skriva om a²-4b = 2
som a² = 2 + 4b.

Båda termerna i högerledet är jämna. Är du med på att summan a² då måste vara jämn?

Visa spoiler

Du kan bryta ut 2 så att du får 2(1 + 2b). Som AlexMu gjorde i #7.

---

Tillägg: 14 dec 2024 19:07

ett tal minus ett jämnt tal borde kunna vara vilket som helst

Frågan gällde om ett tal minus ett jämnt tal blir ett jämnt tal,
vad gäller då om det första talet?

Ja, men jag menar så. Att det borde kunna vara både jämnt och udda. Men det känns lite logiskt att jämnheten i det hela kanske aldrig försvinner?

Men jag tror jag är med på det. I och med att båda talen i HL går att dividera med 2 så går nog a också det. Förutsatt då att ett jämnt tal+ ett jämnt tal alltid är ett jämnt tal 

Och tack, det var fint 🙂

Förutsatt då att ett jämnt tal+ ett jämnt tal alltid är ett jämnt tal 

Känner du någon tveksamhet där?

Louis skrev:

Förutsatt då att ett jämnt tal+ ett jämnt tal alltid är ett jämnt tal 

Känner du någon tveksamhet där?

I och med att man kan definiera eller sätta ett udda tal som ett jämnt tal+1, 2n+1, så borde det betyda att om man aldrig.. plussar eller tar bort 1 från ett jämnt tal att det fortsätter vara jämnt! Så jag är inte direkt tveksam kanske men ska man vara _helt_säker måste man bevisa att det gäller för alla tal?

Att ett tal är jämnt innebär att det innehåller faktorn 2.

Om du adderar två jämna tal kan du skriva summan som 2m + 2n, där m och n är heltal.
Bryt ut 2 så får du 2(m + n). Även summan innehåller faktorn 2 och är alltså jämn. Alltid.

Okej! Då följer det att jag är med på det andra också

AlexMu skrev:

En egenskap som primtal har är att vi inte kan multiplicera ihop två tal för att få ett primtal. När vi kvadrerar ett tal är det exakt vad vi gör, vi multiplicerar ihop tal.
Nya delare till kvadraten kvadraten kommer dyka upp, men eftersom vi inte kan multiplicera ihop tal för att få primtal är det omöjligt att någon av de nya delarna är ett primtal.

Lite mer invecklad förklaring

Jag vet inte om man går igenom detta i bevisdelen i matte 4 men en fundamental egenskap av heltalen är förmågan att faktorisera dem till primtal, så kallad primtalsfaktorisering. Om ett tal inte är ett primtal är det per definition en produkt av andra tal, som i sin tur kanske är primtal eller sammansatta. Om de är sammansatta kan vi fortsätta dela upp dem till faktorer av primtal.

Vi tar exemplet $12$. Vi kanske först ser att $12 = 3 \cdot 4$. 3 är primtal så vi lämnar det där, men $4=2\cdot 2$ och 2 är primtal. Då får vi att $12 = 2\cdot 2 \cdot 3$ och nu har vi hittat primtalsfaktoriseringen av $12$. 

Primtalsfaktorisering av 48

När vi kvaderar $12$ kan vi lika gärna bara kvadrera primtalsfaktorerna. Alltså
$12^2 = 2^2 \cdot 2^2 \cdot 3^2 = 2^4 \cdot 3^2$. Om $12^2$ är delbart med något tal måste det vara delbart någon av primtalsfaktorerna eftersom de representerar exakt samma tal. 
På så sätt kan vi exempelvis se att $12^2$ är delbar med $3^2$ eftersom det är något som går jämnt i primtalsfaktoriseringen. $3 \cdot 2^3$ är också delbar av samma anledning. Men $3^3$ är inte det eftersom vi inte har tillräckligt med treor i talet. 

Det är omöjlgt att nya primtal dyker upp i kvadreringen av ett tal. Den enda skillnaden är att i kvadraten så har gamla primtal i faktoriseringen en högre exponent. Det kan inte dyka upp nya 

Hej igen,

Okej. Alla tal består av primtalsfaktorer när man plockar isär dem tillräckligt. Så länge man inte utför någon annan operation än multiplikation så kommer grundstenarna vara desamma? Eller i varje fall med utökade heltalsexponenter?

Men oggi skriver: "Om a är ett heltal och a^2 är delbart med ett primtal q, så måste även a vara delbart med q, och alltså är a^2 delbar med q^2.

Men 12x12 = 144. 144 är delat med primtalet 9 för det = 16. Då ska det följa att talet a, i det här fallet 12, också är delbart med talet q, som är 9. Men det stämmer ju inte? Och då är 144 också delbart med 81, 144/81 = 1.78? :/ Eller är primtal i den här kontexen specifikt enskilda primtalsfaktorer?

Dkcre skrev:

[...].

Men 12x12 = 144. 144 är delat med primtalet 9 för det = 16. Då ska det följa att talet a, i det här fallet 12, också är delbart med talet q, som är 9. Men det stämmer ju inte? Och då är 144 också delbart med 81, 144/81 = 1.78? :/ Eller är primtal i den här kontexen specifikt enskilda primtalsfaktorer?

Nej, primtal är primtal, oavsett om de är faktorer I ett annat tal eller inte.

Men varken 9 eller 16 är primtal.

====

Talet 144 är delbart med primtalen 2 och 3, men inte med några andra primtal.

Det oggih skriver är att eftersom 12*12 är delbart med 2 och 3 så är även 12 delbart med 2 och 3, och därför är 144 även delbart med 2² = 4 och 3² = 9.

Yngve skrev:

Dkcre skrev:

[...].

Men 12x12 = 144. 144 är delat med primtalet 9 för det = 16. Då ska det följa att talet a, i det här fallet 12, också är delbart med talet q, som är 9. Men det stämmer ju inte? Och då är 144 också delbart med 81, 144/81 = 1.78? :/ Eller är primtal i den här kontexen specifikt enskilda primtalsfaktorer?

Nej, primtal är primtal, oavsett om de är faktorer I ett annat tal eller inte.

Men varken 9 eller 16 är primtal.

====

Talet 144 är delbart med primtalen 2 och 3, men inte med några andra primtal.

Det oggih skriver är att eftersom 12*12 är delbart med 2 och 3 så är även 12 delbart med 2 och 3, och därför är 144 även delbart med 2² = 4 och 3² = 9.

Nej just det, 9 är delbart med 3 naturligtvis..

Jo, okej.