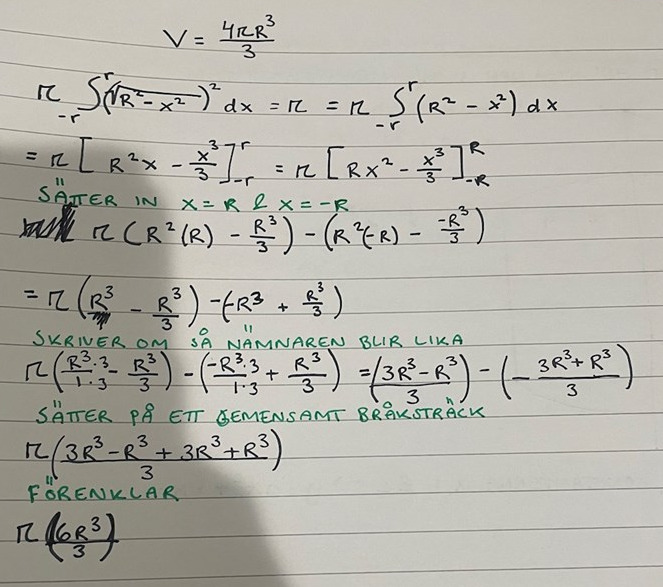Bevis för formeln av volym av klot

Julialarsson321 skrev:

Jag behöver lite hjälp med denna, såhär har jag räknat med jag kommer inte längre. Går det att skriva om detta till (4puR^3)/3? Eller hur fortsätter jag?

Teckenfel på sista termen på raden ovanför "FÖRENKLAR", när du tar bort parentesen blir det - R³.

Så det blir 3R^3-R^3-3R^3+R^3? Blir inte -*- där +? 

Nej, 3R³-R³+3R³-R³

Såhär? Och ska jag verkligen dela med 3 om jag vill få det till (4piR^3)/3? Då försvinner ju nämnaren

Hur får du 3-1+3-1 att bli 3?

Oj det blev fel. Blir det då (6R^3- R^6)/3?

Nej. Gå och lägg dig nu, så räknar du nog rätt i morgon!

Jag har dyskalkuli så dessa små uträkningar är väldigt svåra för mig att räkna ut. Jag får det till 3R^3 + 3R^3 vilket blir 6R^3 och sen subtraherar jag 2R^3 så det blir 4R^3.

Helt rätt - nu har vi hoppat över trean i nämnaren hela tiden, så om du delar med 3 får du ...

Vad menar du med "små uträkningar", förresten? Menar du att de är skrivna med smma storlek på siffrorna som det är på den vanliga texten?

Så jag ska ta (4R^3)/3 så att nämnaren försvinner? 
menar de mindre utryckningarna som att förenkla siffror eller att multiplicera eller subtrahera. De blir ofta fel för mig. 

De blir ju pi(2R^3)?

Du har skrivit med gröna bokstäver SÄTTER PÅ ETT GEMENSAMT BRÅKSTRECK

$\mathrm{\pi }\left(\frac{3{\mathrm{R}}^3-{\mathrm{R}}^3+3{\mathrm{R}}^3+{\mathrm{R}}^3}{3}\right)$, fast vi var väl överens om att det sista tecknet var fel och det borde vara $\mathrm{\pi }\left(\frac{3{\mathrm{R}}^3-{\mathrm{R}}^3+3{\mathrm{R}}^3-{\mathrm{R}}^3}{3}\right)$, och nu har vi förenklat det till $\mathrm{\pi }\left(\frac{4{\mathrm{R}}^3}{3}\right)$, eller hur?

Yes så långt är jag med

Och då är du klar!

Ska jag då multiplicera in pi i ekvationen? Så det blir (4piR^3)/3?

Om du föredrar det på det sättet så går det lika bra, det är ingen betydelseskillnad. Jag föredrar $V=\frac{4}{3}\pi r^3$ med litet r istället.