Bevis
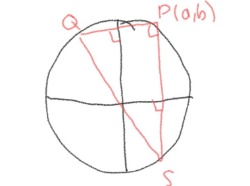
Jag vill visa att tan (-v) = tan (180⁰ - v) , hur går jag tillväga?
Kommer bara fram till detta
Q koordinater --> ( -a , b)
S koordinater --> (a , -b)
Tan v = sin v / cos v
Låt u = -v
Utnyttja att tan(-v) = tan(u) = sin(u)/cos(u)
Det betyder att tan(180-v) = tan(180+u) = sin(180+u)/cos(180+u)
Vad är sin(180+u)?
Vad är cos(180+u)?
jarenfoa skrev:Låt u = -v
Utnyttja att tan(-v) = tan(u) = sin(u)/cos(u)
Det betyder att tan(180-v) = tan(180+u) = sin(180+u)/cos(180+u)
Vad är sin(180+u)?
Vad är cos(180+u)?
Fattar inte hur man kommer fram till det?
Och sin(180+u) respektive cos(180+u) .. är det additionsformeln jag ska utgå från?
Kan du vara lite mer specifik om vilket steg det är du inte fattar?
Ja, additionsformeln är ett bra nästa steg.
jarenfoa skrev:Kan du vara lite mer specifik om vilket steg det är du inte fattar?
Ja, additionsformeln är ett bra nästa steg.
Jag förstår stegen, men inte varför man gjorde så och varför man vill räkna fram sin(180+u) respektive cos(180+u)
Kanske en bred fråga egentligen men det är nog det jag inte hänger med på
Anledningen till att jag gjorde bytet från v till u var att tills vidare slippa minustecknet.
Sådana har en väl dokumenterad förmåga att leda till misstag och är därför bra att undvika om det går.
Anledningen till att man vill räkna ut sin(180+u) och cos(180+u) är att för att det finns en additionsformel som vi kan använda för att göra det. Vad du applicerat den och vad fick du i så fall för resultat?
jarenfoa skrev:Anledningen till att jag gjorde bytet från v till u var att tills vidare slippa minustecknet.
Sådana har en väl dokumenterad förmåga att leda till misstag och är därför bra att undvika om det går.Anledningen till att man vill räkna ut sin(180+u) och cos(180+u) är att för att det finns en additionsformel som vi kan använda för att göra det. Vad du applicerat den och vad fick du i så fall för resultat?
Cos(180+u) blir till
-1 cos u
Sin(180+u) blir till
-1 sin u
Just det.
Så vad blir tan(180+u)?
jarenfoa skrev:Just det.
Så vad blir tan(180+u)?
-1 sin u / - 1 cos u
Fattar inte hur det är beviset?
I facit står det
VL = tan (-v) = sin (-v) / cos (-v) = b-/a = - (b/a)
HL = tan (180-v)
sin (180-v) / cos (180-v) = b / -a = -(b/a)
bump
Jag kommer lite sent nu, men eftersom bevis intresserar mig så kommer här ett försök till förklaring.
Om vi börjar med jarenfoas förklaring så var ni nästan i mål.
Det enda som återstod var att konstatera att
tan(
Nu kan vi använda att
och får då
tan(180-v)==tan(-v) V.S.B.
Vi tittar sedan på facits svar, som bygger på din figur överst med enhetscirkeln.
Det som är intressant är att det fungerar på hela enhetscirkeln vilket är viktigt för att beviset ska fungera.
Om vi tittar på din figur så har vi koordinaterna (a, b) för en vinkel .
Det viktiga här är att förstå att om P har koordinaterna (a, b) så har Q koordinaterna (-a, b)och
S har koordinaterna (a, -b).
Facit börjar med VL och konstaterar att det blir -(b/a) och då är vi i punkten S eller hur.
HL visar punkten Q.
Den grafiska förståelsen som finns i facits svar är viktig och underlättar framtida problemlösningar för dig, men det är också viktigt att förstå jarenfoas algebraiska lösning som är elegant. Han kunde möjligen ha refererat till VL och HL för att få högsta poäng så att säga.


