Bestämt volym största värde

Du skriver lite konstiga saker på vägen, sen blir det rätt för att i sista steget få fel igen.

Konens volym ges av formeln 

$\frac{\pi r^{2}h}{3}$

I det här fallet är h en funktion av r (dvs av x) så vi får

V(x) = $\frac{\pi x^2(9-x^2)}{3}$

innan du deriverar kan du förenkla och lämna konstanta faktorer utanför och då får du

V(x) = $\frac{\pi }{3}(9x^2-x^4)$

som du kan derivera på vanligt sätt, kvotregeln vid derivering behöver du bara använda om du har din variabel i nämnaren, så är det inte här.

Jag bara skrev nollställer och maximumspunkt

sista delen frågade om jag kunde dela med 3

är det inte samma sak ?? Det är min fråga  

för att underlätta derivat?? Har jag fel ?

du kan derivera

$\frac{\pi }{3}(9x^2-x^4)$

som det är.

Det du skrev på sista raden i din uträkning

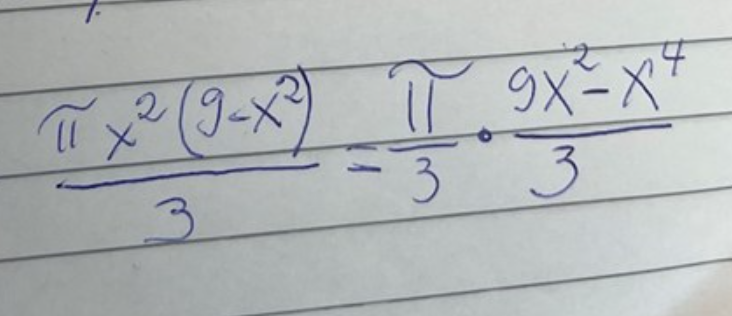
stämmer inte, det har blivit en 3a för mycket i nämnaren

Nu, förstår tack

Nu har jag derivera produkt 

V’= 0 + pi/3 * 18x-4x^3

stämmer det ?

Annabel29 skrev:

Nu har jag derivera produkt 

V’= 0 + pi/3 * 18x-4x^3

stämmer det ?

sånär som på en parentes är det rätt!

V’= pi/3 * (18x-4x^3)

Nästa steget

ska V’(2)= pi/3* (18*2-4(2)^3= pi/3* (4)= 4,19

stämmer?

Annabel29 skrev:

Nästa steget

ska V’(2)= pi/3* (18*2-4(2)^3= pi/3* (4)= 4,19

 

stämmer?

Om du ska söka vilket x-värde som ger största möjliga volym, ska du leta efter derivatans nollställen, och sen undersöka vilka av dessa som ger ett max.

Du menar 

0=pi/3*(18x-4x^3)

18x-4x^3= 3/pi

löser ut x 

stämmer ?

Var kommer 2 ifrån?

Börja med att hitta derivatans nollställen!

-2 och 2 kommer från grafen 

när y=0

om y = 0, dvs att konen inte har någon höjd så är y = 9-x² = 0 och x är +- 3,

men varför bryr du dig om det?, uppgiften är väl att hitta största möjliga volym hos konen under villkoret att basytans periferi tangerar kurvan y = 9-x² ? !

Lite förvirrad 😐 så gör komplicerat 

men måste hitta nollställen

och det är när V’= 0 

tänker jag korrekt?

Då sammanfattar vi lite,

Du har kommit fram till att konens volym som funktion av x kan beräknas som 

V(x) =$\frac{\pi }{3}(9x^2-x^4)$för att hitta största möjliga värde deriverar vi funktionen och får då

V'(x) = $\frac{\pi }{3}(18x-4x^3)$

lokala max och min hittar vi vid derivatans nollställen alltså löser vi ut x ur ekvationen

0 = $\frac{\pi }{3}(18x-4x^3)$

Dela bägge led med pi/3 så får vi 

18x-4x³ = 0, som vi kan skriva som

x( 18-4x² ) = 0

Vi ser att ett nollställe får vi vid x = 0, (det ger volymen 0, som rimligen är en minpunkt)  det andra nollstället får vi om

18-4x² = 0

dvs x² = 18/4

Kan du fortsätta härifrån?

Ja, tack 

Svaret blir x= 2,14 e 

jag har en fråga 

i grafen får man x och y 

vad ska jag använda dessa värde ???

För den jag har förstått när man deriverar då ska man hitta största värde, stämmer det ?

Det du räknat ut så här långt är för vilket x-värde som konen har sin största volym, återstår att räkna ut den volymen!

Mu förstår jag först måste hitta på vilket x värde har funktionen största värde , men jag vill veta  volym 

om det skulle istället leta efter minsta värde ? 

Jag tror du fick fel nånstans på vägen när du beräknade volymen

för x² =18/4 =9/2 = $\pm \frac{3}{\sqrt{2}}$, har volymen ett största värde

Vi har från inlägg #15 att

V(x) = $\frac{\pi }{3}(9x^2-x^4)$

om vi sätter in vårt värde på x får vi

$$\begin{gathered} \frac{\pi }{3}(9\frac{9}{2}-{\left(\frac{9}{2}\right)}^2) = \frac{\pi }{3}(\frac{81}{2}-\frac{81}{4}) = \\ =\pi \frac{81}{12} \approx 21,2 \end{gathered}$$

Annabel29 skrev:

om det skulle istället leta efter minsta värde ? 

Om du vill ta reda på volymens minsta värde gör du till en början på samma sätt:

1. Ta fram ett uttryck för volymen V som endast beror på en variabel x.
2. Derivera detta uttryck, dvs ta fram.V'(x).
3. Sätt derivatan lika med 0 och lös ekvationen: V'(x) = 0.
4. Då får då fram ett eller flera nollställen. Dessa kan vara minimi-, maximi- eller terasspunkter.
5. Du kan nu om du vill bestämma dessa nollställens karaktär med hjälp av teckentabell eller andraderivata.
6. Eller så tar du helt enkelt fram motsvarande volymer och ser vilket/vilka av desa värden som är störst/minst.
7. En viktig sak att tänka på är dock att den matematiska modellen (dvs uttrycket för volymen) inte tar hänsyn till uppgiftens förutsättningar. I det här fallet att det ska vara en kon. Finns det något/några värde/n på x som gör att det inte längre är en kon?

Nu har fått samma svar 👍🏽

tack