bestämma värdet på en konstant för att olikhet ska gälla.
Hej,
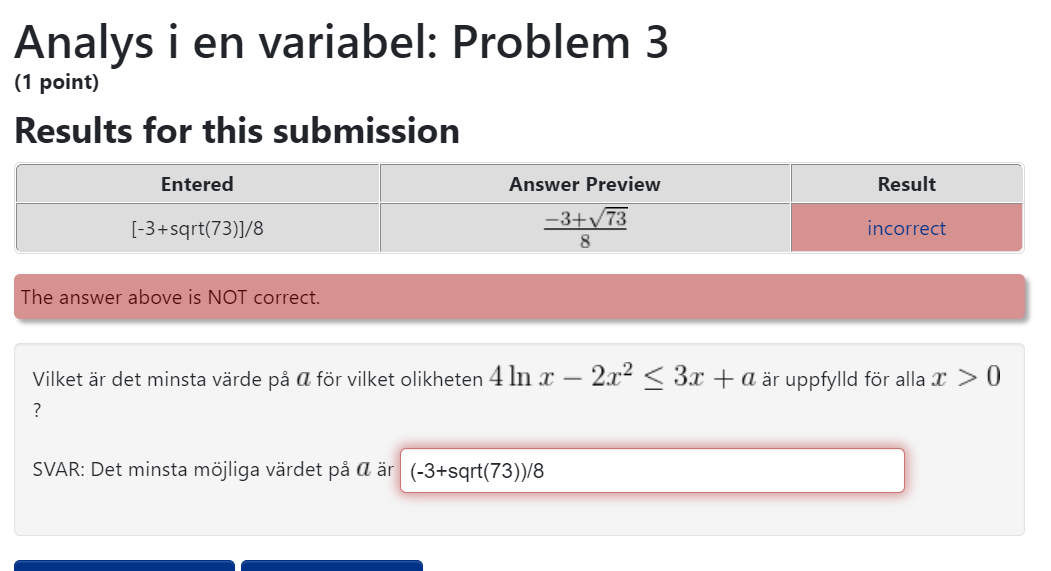
Jag har försökt att lösa denna uppgift. Här nedan är en bild på mitt lösingsförlag. Min tanke med läsningnen är att jag flyttar över 3x+a till VL. Därefter låter hela VL utgöra en funktion. Därefter är min tanke att jag ska derivera och ta fram nollställena som förhoppningsvis är maxvärden och sedan visa att maxvärden är mindre än lika med noll.
Därefter ta fram värdena för punkten och räkna hur mycket jag kan öka/minska värden på konstanten a för att det ska uppfylla funktionen är mindre än eller lika med noll för alla x (större än noll).
Men jag kommer inte vidre in min lösning eftersom att jag har svårt att ta fram det exakt värdet i mina maximipunkter. Kan man lösa uppgiften genom min lösningsmetod eller finns det något annan metod att föredra?

När du flyttar över allt till VL i början ska det vara -a
Jag får som du (fast jag bryr mig bara om positiva x).
Olikheten kan skrivas
a ≥ –2x2 – 3x + 4 lnx
Sätt högerledet till f(x)
f’(x) = –4x – 3 + 4/x
= –(4x2 + 3x – 4)/x
x > 0 så det räcker att teckenstudera nämnaren
–4(x2 + 3x/4 – 1) = 0
En positiv rot r = (–3 + sqr 73)/8
Tecken
x r
f’ + 0 –
f väx. f(r) avt.
Och i likhet med dig känner jag måttlig entusiasm inför att beräkna f(r).
Antingen har vi tänkt fel, eller också finns en smartare metod.
Marilyn skrev:Jag får som du (fast jag bryr mig bara om positiva x).
Olikheten kan skrivasa ≥ –2x2 – 3x + 4 lnx
Sätt högerledet till f(x)
f’(x) = –4x – 3 + 4/x
= –(4x2 + 3x – 4)/x
x > 0 så det räcker att teckenstudera nämnaren
–4(x2 + 3x/4 – 1) = 0En positiv rot r = (–3 + sqr 73)/8
Tecken
x r
f’ + 0 –
f väx. f(r) avt.
Och i likhet med dig känner jag måttlig entusiasm inför att beräkna f(r).
Antingen har vi tänkt fel, eller också finns en smartare metod.
Tack Calle "-a". Tack Marilyn, nu när du säger det så kommer jag på att jag inte behöver undersöka x<0 inte bara för att uppgiften säger det utan också för att det inte existerar för funktionen för att den innehåller en lnx term.
Håller med dig Marilyn, tror att jag borde få rätt svar om räknar ut f( (-3+sqrt73)/8) och därefter kollar vilket värdet jag behöver ge till a för att max-punkten ska gå igenom x-axeln.
Men att göra den uträckningen känns väldigt arbetssam, måste finns en annan metod som man ska använda.
2x2 - 4•ln(x) = 2(x2 - ln(x2)) >= 2
Jan Ragnar skrev:2x2 - 4•ln(x) = 2(x2 - ln(x2)) >= 2
Aha, det kanske leder nånvart, intressant!
Ragnar, jag förstår din omskrivning. Men jag förstår inte hur det ska hjälpa mig att lösa uppgiften?
Förstår heller inte varför du skriver 2x^2-4lnx nör jag har 4lnx-2x^2 i VL. Tänker du att jag ska flytta över till högerledet och göra något där?
Hur ska jag lösa uppgiften?
4•ln(x) - 2x2 = -2(x2 - ln(x2)) <= -2 <= 3x + a
Det minsta skillnaden inträffar för x = 1. Då måste a >= -5.
När jag kollar mot WolframAlpha stämmer det inte med -5. Värdet verkar ligga på ungefär -4,5 så något har jag missat.
Jan Ragnar skrev:4•ln(x) - 2x2 = -2(x2 - ln(x2)) <= -2 <= 3x + a
Det minsta skillnaden inträffar för x = 1. Då måste a >= -5.
Precis! Försökte med lite uträkningar här nere. Jag kommer dels fram till att x inte kan vara noll. Men då x närmar sig 0, så kommer lnx att närma sig -oändligheten. Men lyckades inte så fram något.
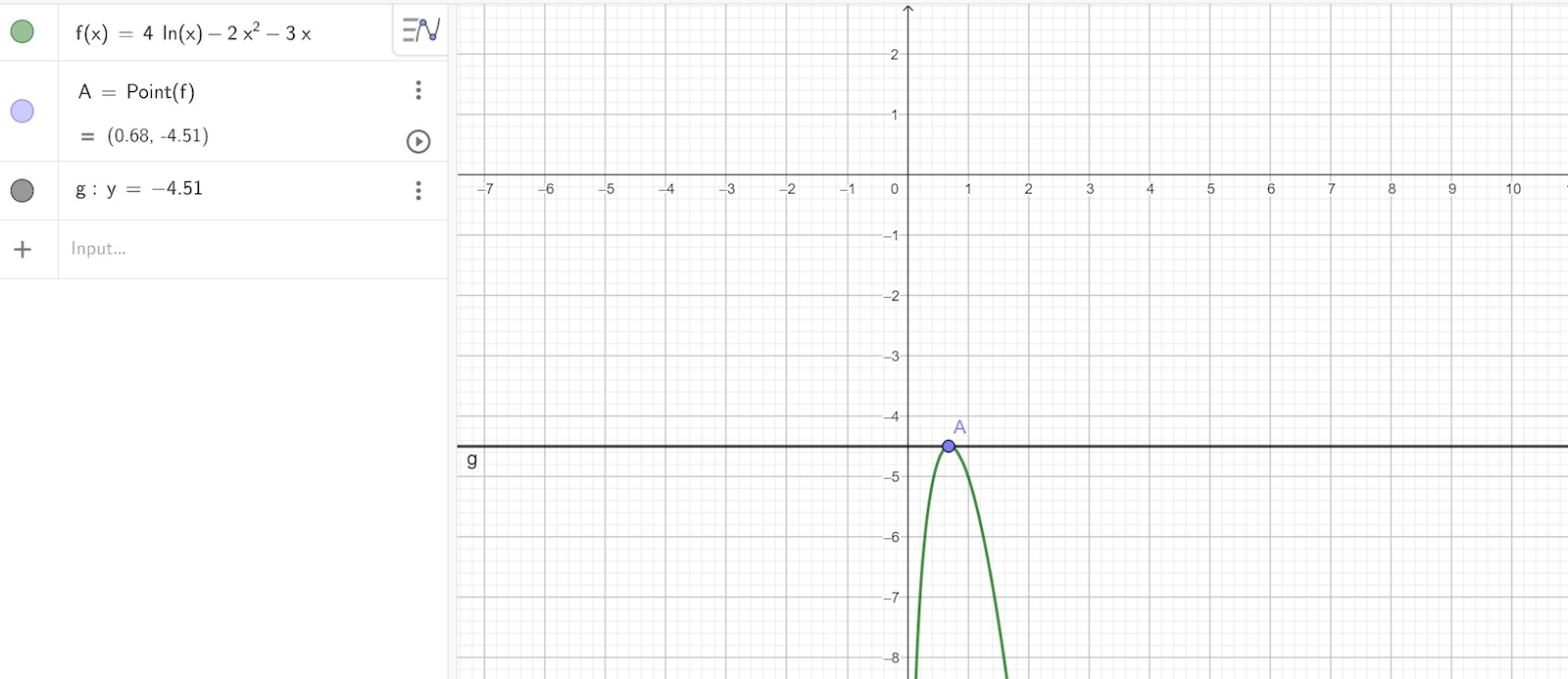
Tanke slog mig att jag skulle räkna ut gränsvärdet för ”funktionen” då den går mot 0+ samt +oändlighet. Dock vet jag inte hur jag ska göra det?
Något tips på hur jag ska gå vidare? 
När jag slår in philip22:s och mitt värde (med roten ur 73 mm) på räknaren (r ≈ 0,693000468) och beräknar f(r) så får jag att minsta värdet för a ≈ –4,506399119.
Nåt lurt är det.
Marilyn skrev:När jag slår in philip22:s och mitt värde (med roten ur 73 mm) på räknaren (r ≈ 0,693000468) och beräknar f(r) så får jag att minsta värdet för a ≈ –4,506399119.
Nåt lurt är det.
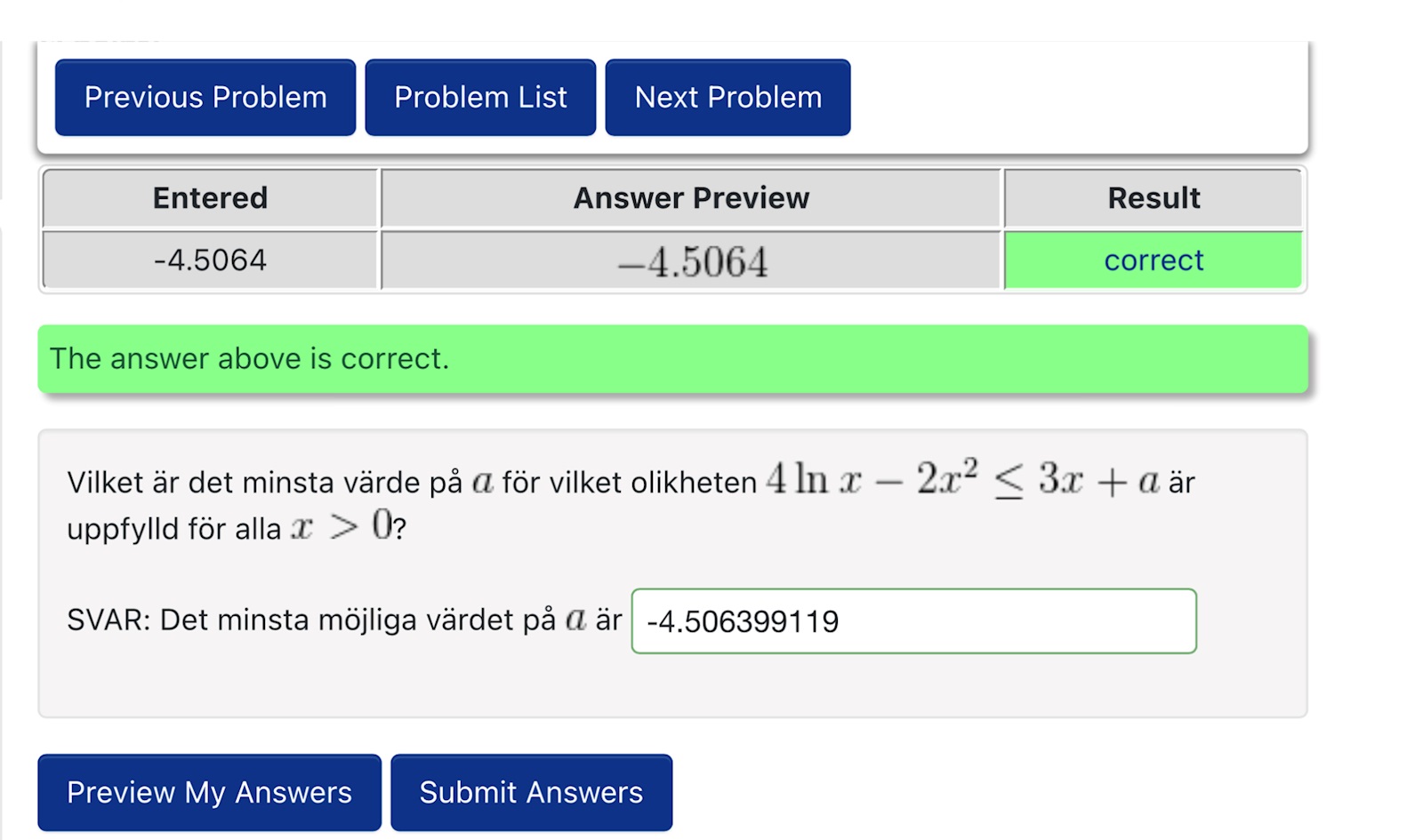
- Satta in det som svar och fick rätt!
Ibland får man bita i det sura äpplet…
Det minsta a som för positiva x är ≥ –2x2 – 3x + 4 lnx
är amin = 4 ln [ (–3 + sqr73)/8 ] – (23 + 3 sqr73)/16 ≈ –4,506 399 119

Tillägg: 23 nov 2023 16:53
(philip22, du får gärna berätta ifall detta var fel. Eller rätt.)
Marilyn skrev:Ibland får man bita i det sura äpplet…
Det minsta a som för positiva x är ≥ –2x2 – 3x + 4 lnx
är amin = 4 ln [ (–3 + sqr73)/8 ] – (23 + 3 sqr73)/16 ≈ –4,506 399 119
Tillägg: 23 nov 2023 16:53
(philip22, du får gärna berätta ifall detta var fel. Eller rätt.)
Yes, det som du svarade är rätt! Tack för all hjälp!
OK, i verkligheten kan man ibland behöva bana sig väg i otillgänglig terräng. Men i matematiken tycker jag man bör slippa sådant.



