Bestämma en funktions extrempunkt

Uppgiften jag fastnat på ser ut som följande: 

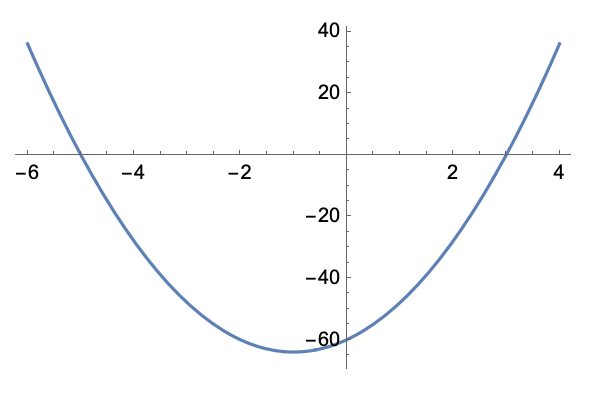
En andragradsfunktion definieras av g(x) = 4(x – 3)(x + 5). Bestäm funktionens extrempunkt och avgör dess karaktär. (Utan digitala hjälpmedel)

För att få fram svaret började jag med att skriva om ekvationen till pq-form:

x^2+2x–15=0

Sedan fick jag med hjälp av pq-formeln ut att:

X1=3 och X2=–5

Därifrån räknade jag ut Xsymmetri:

(3–5)/2=–1

Jag skrev sedan ut andragradsfunktionen som jag fått i uppgiftsbeskrivning som en ekvation med g(x)=Xsymmetri:

–1=4(x–3)(x+5)

= –1=4x^2+8x–60

Det är härifrån jag har svårt, för allt jag får när jag räknar är olika tal som, i min värld i alla fall, inte går att räkna utan digitala hjälpmedel. Exempel på vad jag fått fram är:

59=4x^2+8

4x(x+2)–59=0

x^2+2x=59/4

59 blir ju odelbart pga att det är ett primtal men jag vet inte om jag gjort något fel på vägen eller om hela min metod är fel, men skulle vara mycket tacksam om någon skulle kunna förklara hur jag borde tänka.