Bestämma ekvation för tangent

Hur får du "x var ju 0, och då blir y 1"?

"I punkten 0,0 är lutningen 1. Är då x=1 i den deriverade funktionen?" hänger jag inte heller med på.

Den funktion du ska hitta tangenten till är y = sin(x). Du hittar lutningen genom att hitta y'(0), men skärningen med y-axeln är i punkten ( 0 , y(0) ). :)

virr skrev:

Jag förstår inte riktigt varför svaret ska bli det det blir, misstänker att det är för att jag inte förstått frågan korrekt. Frågan lyder: Bestäm ekvationen för tangenten till y= sin x i punkten (0,0). Detta är b-frågan till att man skulle bestämma lutningen, och det var inget problem, om y= sin x är y'= cos x, och i punkten 0,0 blir lutningen alltså 1. Men i andra frågan tänkte jag att svaret skulle vara y'(0)= cos (0). Svaret ska vara y=x , och facits ledtråd förklarar med y=kx+m , k= 1 och punkten 0,0 ger att m=0. Men x var ju 0, och då blir y 1, dvs k=0 ger 0*1 + m??? Eller ska man vända på det efter att man har deriverat ursprungsfunktionen? I ursprungsfunktionen är x=0. Man efterfrågar vad derivatan är, dvs lutningen. I punkten 0,0 är lutningen 1. Är då x=1 i den deriverade funktionen? Är det inte fortfarande så att vi befinner oss på 0 i x-led, men att 1 i y-led indikerar lutningen i ursprungsfunktionen?

Standardfråga 1a: Har du ritat?

Om du gör det, kommer du att se att tangenten till funktionen y=sin(x) i punkten (0,0) är en rät linje genom origo med lutningen k=cos(0)=1, d v s y=x.

Jag fick rätt på frågan om lutningen enl boken, men jag kanske uttrycker mig felaktigt om den ändå. Hrm. Det jag menar är att efter y= sin x är y'= cos x. När sinus av x är 0 när x är 0, och då är cosinus 1. Om derivatan av sin x = cos x, vilket den är i mitt formelblad, är lutningen för sinuskurvan 1 när sinuskurvan är på punkten 0,0. Är det fel?

Min fråga handlade egentligen inte om det, utan om följdfrågan där man ska bestämma ekvationen för tangenten i det ovan. Och ok, när y är 1 är ju x noll, om man tänker y och x  som sinus och cosinus i enhetscirkeln.

Pepparkvarn, menar du att jag jobbade (felaktigt) med y'-funktionen istället för y-funktionen? Att när man ska bestämma en ekvation för något ska man... vad är det man ska göra? Förlåt, jag hänger inte riktigt med. Minns att jag gjorde det här i matte 3, men det har varit ett visst uppehåll.

Tangenten är uppenbarligen en rät linje som tangerar funktionskurvan i en tangeringspunkt.

I ditt fall är tangeringspunkten origo =(0,0).

Tangentens ekvation: $y=kx+m$, där

k (tangentens riktningskoefficient)=förstaderivatans värde i tangeringspunktens  x-koordinat, dvs i ditt fall

$k=y^\prime (0)$.

Är du med på detta ?

Återstår att bestämma m, dvs det y-värde där tangenten skär y-axeln.  Ok?

Denna tankegång kan du använda på liknande uppgifter. Testa gärna något liknande exempel.

virr skrev:

Jag fick rätt på frågan om lutningen enl boken, men jag kanske uttrycker mig felaktigt om den ändå. Hrm. Det jag menar är att efter y= sin x är y'= cos x. När sinus av x är 0 när x är 0, och då är cosinus 1. Om derivatan av sin x = cos x, vilket den är i mitt formelblad, är lutningen för sinuskurvan 1 när sinuskurvan är på punkten 0,0. Är det fel?

Så här långt är det rätt.

 

Min fråga handlade egentligen inte om det, utan om följdfrågan där man ska bestämma ekvationen för tangenten i det ovan. Och ok, när y är 1 är ju x noll, om man tänker y och x  som sinus och cosinus i enhetscirkeln.

I enhetscirkeln ja, men det här är kurvan y=sin(x). Det kanske är samma y, men det är inte alls samma x. x i sin(x) är en vinkel.

Smaragdalena: Det är mycket möjligt att jag är en överkänslig person, men nästan varje gång du svarar mig känns det som en pisksnärt. Det som är uppenbart för dig är inte uppenbart för mig. I det här fallet var det inte uppenbart för mig att tangenten var en rät linje (menar ni rät horisontell linje? - saksamma, jag återgår till den faktiska frågan i ett annat inlägg). Nästan varje gång du svarar mig med dina "standardfrågor" känns det lite som att vara en hundvalp som får nosen tryckt i det den ska lära sig att inte göra. Samma sak när du drar till med att jag måste göra si eller så för att ni ha en sportslig chans att fatta vad jag talar om. Jag kommer av mig och får jobba ett tag med obehagskänslan innan jag kan fortsätta lära mig matte. Jag *vet att det är bra att rita. Du har tydliggjort det oerhört starkt. Men jag vet också att din pedagogik inte hjälper mig. Jag blir tilltryckt. Jag uppskattar det inte. Kan du på något vis finna ett sätt att modifiera hur du uttrycker dig, eller bara låta bli att svara mig, skulle jag verkligen uppskatta det. Jag har försökt ignorera det här länge nu, och anpassa mig i vad jag delger för information i mina frågor, men åter åter igen stjäler det här så j-kla mycket energi från mig. Som sagt - måvara att jag är extremt överkänslig. Men ändå.

Att en tangent är en rät linje som tangerar en kurva lär man sig i Ma3. Eftersom du skriver i Ma4 bör du känna till detta. En rät linje behöver inte vara horisontell - en rät linje kan skrivas på formeln y=kx+m (om den inte är vertikal, då är det x=konstant).

Du behöver kunna Ma3 för att kunna lära dig Ma4 - det är ingenting som varken du eller jag kan ändra på, det är fakta. Mattekurserna bygger på varandra, och om man inte kan en kurs är det meningslöst att ge sig in på nästa kurs.

Gå tillbaka och repetera Ma3, kanske Ma2 och rentav Ma1 också om du vill ha en chans att lära dig Ma4.

Om du vet att du borde rita - varför gör du inte det?

Att försöka lära sig Ma4 utan att ha en stabil grund är som att bygga en skyskrapa i centrala Göteborg utan att påla ner genom leran till fast berg - det kommer att rasa förr eller senare.

Dvs du tänker inte ta till dig någonting av det jag skrev. Jag har blivit godkänd på matte 3. Jag läser de facto matte 4 nu. Jag förstod inte frågan. Du är inte hjälpsam. Du är inte pedagogisk. Jag tycker synd om dina elever. Vänligen avstå från att svara när jag ställer frågor.

Inte den tonen tack, virr! Att be en användare uttrycka sig mjukare är helt okej, men detta:

Du är inte hjälpsam. Du är inte pedagogisk. Jag tycker synd om dina elever. Vänligen avstå från att svara när jag ställer frågor.

Är inte okej. // Pepparkvarn/Smutstvätt, moderator

Ok, jag kan acceptera det, men det är en reaktion på att jag får noll respons på problemet. Vet inte vad annat jag kan göra. Det är sk*tjobbigt om och om igen. Nu anlände min privatlärare, så kan inte svara på ett tag. 

Du har inte fått "noll respons på problemet", du verkar t o m ha fått reda på vad det är som är felet - att du inte vet vad en tangent är och inte hur man skall skriva formeln fören rät linje. Om du ritar upp en sinuskurva kan du se att dess lutning varierar hela tiden.

Vi har funktionen f(x) = sin(x), och vi håller oss runt punkten x = 0. Vi ritar upp funktionen och en uppskattad tangent:

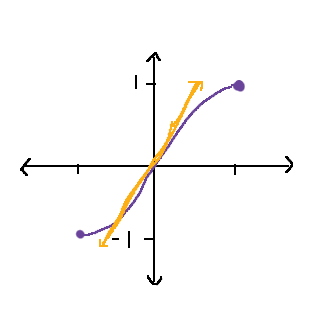
Vi vill hitta tangenten till f(x), liksom alla tangenter har en tangent formen y = kx + m. k är lutningen, den tar vi fram genom att hitta derivatan av f i punkten x = 0, eftersom f'(x) är lutningen hos f i varje punkt x. f'(x) = cos(x). f'(0) = cos(0) = 1.

Då har vi tangenten y = 1x + m = x + m. m är förskjutningen i y-led hos tangenten, och vi behöver då hitta en punkt på grafen till tangenten. Eftersom vi inte har tangentens ekvation, tar vi punkten där y och f(x) sammanfaller, vilket sker då x = 0 (eftersom det är där vi beräknar tangenten). f(0) = sin(0) = 0. Tangenten skär då punkten (0, 0), och vi kan sätta in punkten i tangentens ekvation:

0 = 1*0 + m, vilket ger att m = 0. 

Vi har då tangenten y = x, till funktionen f(x) då x = 0. 

Ett alternativ här är annars enpunktsformeln, vilken ger:

$y-y_1=k(x-x_1)$

där $y_1=f(x_1)$

Jag har löst problemet. S: jo, det vet jag visst, men jag missförstod frågan. Och jag vidhåller att jag inte orkar kommunicera med dig - jag mår inte bra av det. Eftersom du inte vill ta till dig av det, och inte vill sluta skriva till mig, får jag väl helt enkelt sluta använda forumet. Tack.

Det verkar som om det är läsförståelse du behöver träna på. Gå och låna en rolig bok på biblioteket och läs den - det kommer att hjälpa dig i dina mattestudier!

Jag måste bara påpeka hur j-kla elak din sista kommentar var. Jag har alldeles utmärkt lösförståelse, och mina bokhyllor rymmer allt från Beckett till Proust. Dock har jag en ganska jobbig period i livet just nu, där hjärnan uppenbarligen inte fungerar på topp, men jag ändå försöker utvecklas och lära mig. Du har inget som helst anledning att hunsa mig som en elev (-och jag tycker inte man ska hunsa elever). Och du har ingen som helst anledning att bry dig om vilket tidsperspektiv eller vilken ordning jag intar kunskap. Jag tror inte någon hjälps av elaka tjuvnyp, och jag får i alla fall kortslutning av sådana just nu. Jag pallar inte med dem helt enkelt. Problemet jag påpekade handlade alltså inte om matte. Men jag fortsätter lära mig matte.

Det verkar i alla fall som om du inte lyckades tyda vad det stod i uppgiften - alltså är det läsförståelsen som brister, inte dina räknefärdigheter. Läsförståelse är jätteviktig i matte, t  m viktigare än att rita!

Och min kommentar var absolut inte menad att vara elak - den var menad som hjälp. Förstår du inte det, så tyder även detta på att du behöver träna på din läsförståelse.

Jag tyckte du behövde träna på din ton. Det var den jag opponerade mig emot. Men ok, jag släpper det här. Som sagt, är extra känslig just nu, och orkar inte med konflikter. Jag förstår att det är viktigt att läsa noggrant och reflektera över vad som efterfrågas. Det är svårare när man blir stressad. Så det jobbar jag på. 

Jag blir riktigt ledsen över att du kan missförstå mitt vänligt menade råd på det sättet.

Det är ingenting jag önskar. Men kan du förstå att (bl.a) det där med "standard fråga 1" om och om ingen som svar kan upplevas som jobbigt? Alltså som sagt, jag erkänner att jag är överkänslig just nu. Har hållit på att driva mig in i väggen senaste tiden med heltidsjobb och dumt jäktade pluggprojekt (med mera). Men ja.. Det var i alla fall upplevelsen jag försökte förmedla, och att jag då hellre avstod hjälpen, för tonen gjorde att jag gång på gång fick sluta räkna och hantera obehagskänslorna innan jag kunde fortsätta. Men det är såklart inte lätt det här att förmedla sig skriftligt och läsa av rätt. Jag accepterar att din avsikt var att hjälpa.

Det är så jättevanligt att folk inte har ritat, så jag har varit lat nog att använda en standardformulering - jag trodde att folk skulle se den i många trådar och förstå att det inte var någon tyken fråga utan ett standardsvar som alla som inte har ritat får. Har jag tänkt fel? Hur bör jag formulera mig istället?

Tillbaka till problemet. Hur vet vi att y = x är en tangent till kurvan i den givna punkten? Det vill säga hur definierar man egentligen matematiskt att två kurvor tangerar varandra i en punkt? Det är lätt att se visuellt, men hur uttrycker man det precist matematiskt?

Jag skriver detta för att jag såg att detta diskuterades väldigt ihärdigt av några lärare på nätet. Alla hade sin teori, men de kunde inte riktigt ge en klar definition.

Jag letade i en massa böcker innan jag hittade en som faktisk gav en definition av detta begrepp.