Bestämma ekvation för plan som tangerar sfär
Halloj!
Jag sitter med uppgiften nedan:

Jag har tänkt så här:
Linjen borde på vektorparametrisk form kunna skrivas . Vi låter .
Låt tangeringspunkten mellan sfären och planet vara . Om vi bildar en godtycklig vektor från tangeringspunkten och en punkt i planet, kommer denna också ligga i planet. Vi väljer punkten som den andra punkten och erhåller då:
Vi inser att kommer utgöra en normal till planet. Vi har då att:
Nu kan man ställa upp ett ekvationssystem:
Här har vi dock inte tillräckligt med information för att lösa ekvationssystemet. Betyder det att jag bara kan välja vilka värden jag vill på och så länge mina motsvarande och blir reella?
En sak jag dock tänkte på var att om man har två punkter i ett plan och en normal till planet har koefficienterna har vi att:
Kan det vara användbart här? Vi har ju faktiskt två punkter (varav en är tangeringspunkten!) och koefficienterna uttryckta i tangeringspunktens koordinater.
Nu skummade jag igenom din lösning snabbt bara men det ser inte ut som att du har nyttjat det faktum att punkten (x0,y0,z0) ligger på sfären.
EDIT: Jo det är ju första ekvationen i systemet.
Av symmetri vet du att y0=0, dvs tangeringspunkten bör vara (x0,0,z0).
Jag hänger inte riktigt med. Vad menar du med av symmetri?
Föreställ dig sfären och linjen i 3D. Planet är ett godtyckligt plan som kan roteras med linjen som symmetriaxel. Vi vill hitta rotationen sådan att planet tangerar sfären.
Här har du scenariot sett från positiva z-axeln.
Här har du scenariot sett från negativa y-axeln. Som du ser kommer det finnas 2 möjliga lösningar.
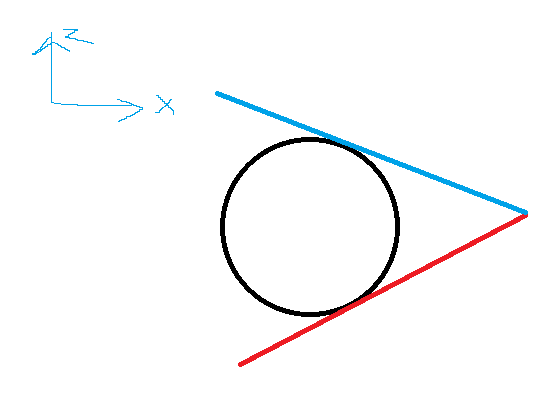
Tillägg: 22 okt 2024 15:45
Linjen går i riktning ut/in genom skärmen i den punkt där den blåa och röda linjerna skär varandra.
Jag känner att jag är alldeles för trött i huvudet för att föreställa mig saker i 3D (har sovit typ 2 timmar...). Finns det något sätt att komma fram till att rent algebraiskt istället? Kan man tänka att eftersom normalen saknar -koordinat måste det säga något om hur planet ligger i rummet?
Bra fråga. Att normalen till planet saknar y-komponent är bara en följd av att planet spänns upp av en vektor som löper i y-riktningen (denna vektor är just linjen). Jag kan inte komma på något bra algebraiskt argument just nu.
Jag vet att du gärna vill göra algebraiska metoder, det känns som att lösningen blir mer vattentät då (så känner jag med). Men faktum är att intuitiva symmetriargument används väldigt ofta i dessa typer av kurser, och det är inte bara godkänt att göra så utan man uppmanas till och med att göra så i många sammanhang.
Så hur luddigt det än låter är jag rätt säker på att motiveringen
"Eftersom att scenariot är symmetriskt med avseende på xy-planet beläget i y=0 vet vi att tangeringspunkten ska ligga i planet y=0 och därmed gäller det att y0=0"
är tillräckligt bra för att erhålla full poäng på en sån här uppgift på en tenta.
Borde man inte kunna säga att om normalen saknar -komposant så är planet beläget i -planet? Och då löper det alltså parallellt med -axeln, alltså måste , eftersom tangeringspunkten måste ligga på -axeln då. Det vill säga, tangeringspunkten måste vara någon av de svarta punkterna:
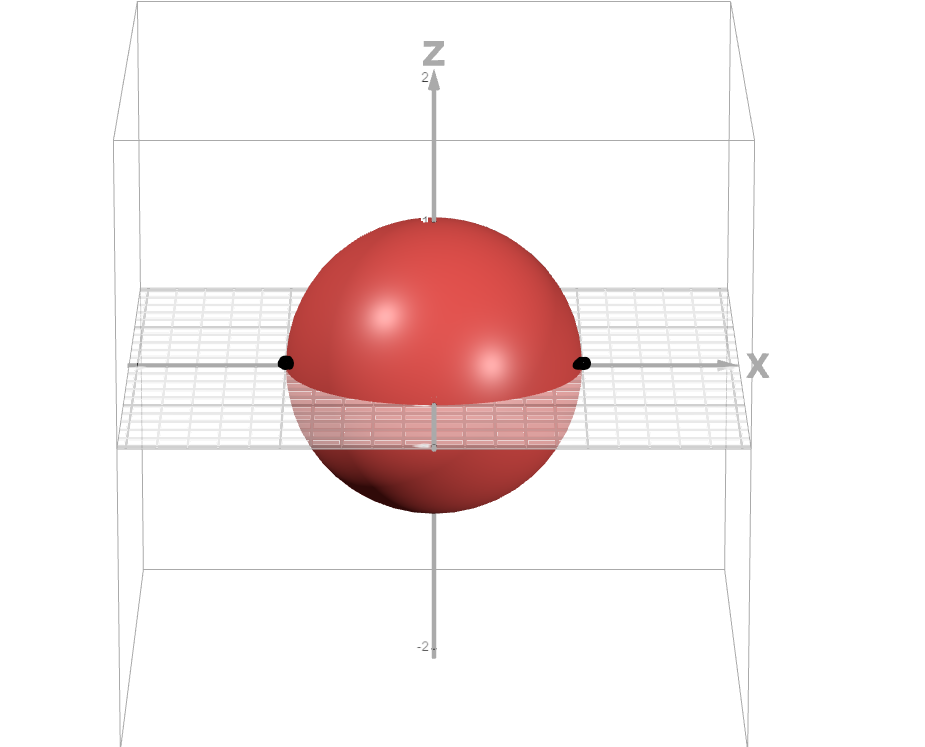
(kanske är det som du menade med dina ritningar, men jag har inte hunnit internalisera dem än)
EDIT: nej, nu när jag grafar ser jag att det såklart inte stämmer. Kan man tänka så här:
Eftersom båda punkterna ligger på en linje som är parallell med y-axeln, måste eftersom planet inte kan gå genom båda dessa punkter annars?
Vill man lösa det här mer "algebraiskt" kan man tänka så här; vi har tre punkter , samt . Eftersom tangeringspunkten ligger på enhetssfären kan också betraktas som en normal till tangentplanet med längden . Det ger oss följande ekvationer
(1) Varje vektor i planet ska vara vinkelrät mot normalen
(2) Varje vektor i planet ska vara vinkelrät mot normalen.
Eftersom ger ekvation (1) och (2) systemet
Som har lösningarna
Normeringsvillkoret ger sedan två möjliga värden på .
Vad menas med att vi betraktar en punkt som en normal? En punkt har väl ingen utbredning i rummet?
Punktens koordinater är vilket kan betraktas som en lägesvektor från origo till punkten.
Lägesvektorn går i normalens riktning (dvs utgör en normal till sfären), dessutom gäller att dess längd är 1 eftersom
Du har förövrigt helt rätt i att man måste skilja mellan punkter i rummet och vektorer, men i vissa fall kan man ta lite genvägar :)
Jaha okej, jag tror jag kan köpa det. Så det vi utnyttjar är att en normal till sfären i tangeringspunkten måste vara en normal till planet också, eller hur?
Japp, det stämmer!
Nice, då är jag med!
Tack så mycket till er båda!
Jag är ett fan av den algebraiska lösningen, men bara så att jag förstår ditt argument också Calle_K:
Menar du att eftersom punkterna som linjen löper genom ligger i "höjd" med y-axeln så måste y-koordinaten för planet vara noll?
naytte skrev:Jag är ett fan av den algebraiska lösningen, men bara så att jag förstår ditt argument också Calle_K:
Menar du att eftersom punkterna som linjen löper genom ligger i "höjd" med y-axeln så måste y-koordinaten för planet vara noll?
Punkterna hade kunnat vara placerade var som helst, det viktiga är att linjen mellan dem är parallell med y-axeln.
Det vi väsentligen gör med symmetriargumentet är att vi projicerar ned rummet på XY-planet för y=0 (alltså planet y=0 som jag ritade i svar #6). Nu har vi ett 2D problem och vi vill bestämma linjen som skär punkten (x,z)=(2,0) sådan att den tangerar cirkeln x2+z2=1. Vi skulle kunna säga att vi har projicerat bort y-dimensionen då denna inte har någon betydelse för svaret.
Tillägg: 22 okt 2024 17:01
Notera att om vi istället hade sfären x2+(y-1)2+z2=1 hade vi inte haft någon symmetri kring planet y=0. Dock hade vi haft en symmetri kring planet y=1 och vi kan sätta y0=1 och sedan fortsätta enligt tidigare.
Denna metod är mer av ett "knep" än en generell metod. Så det bästa kanske är att lära sig en generell approach. Dessutom skulle det inte gå att göra dessa knep i högre dimensioner (hela poängen grundar sig i att man kan visualisera rummet).
Oj, ja jag menade parallell. Men bra, då tror jag att jag förstår. Så man tänker bort -dimensionen helt och hållet och reducerar problemet till en linje och en cirkel istället för en plan och en sfär?
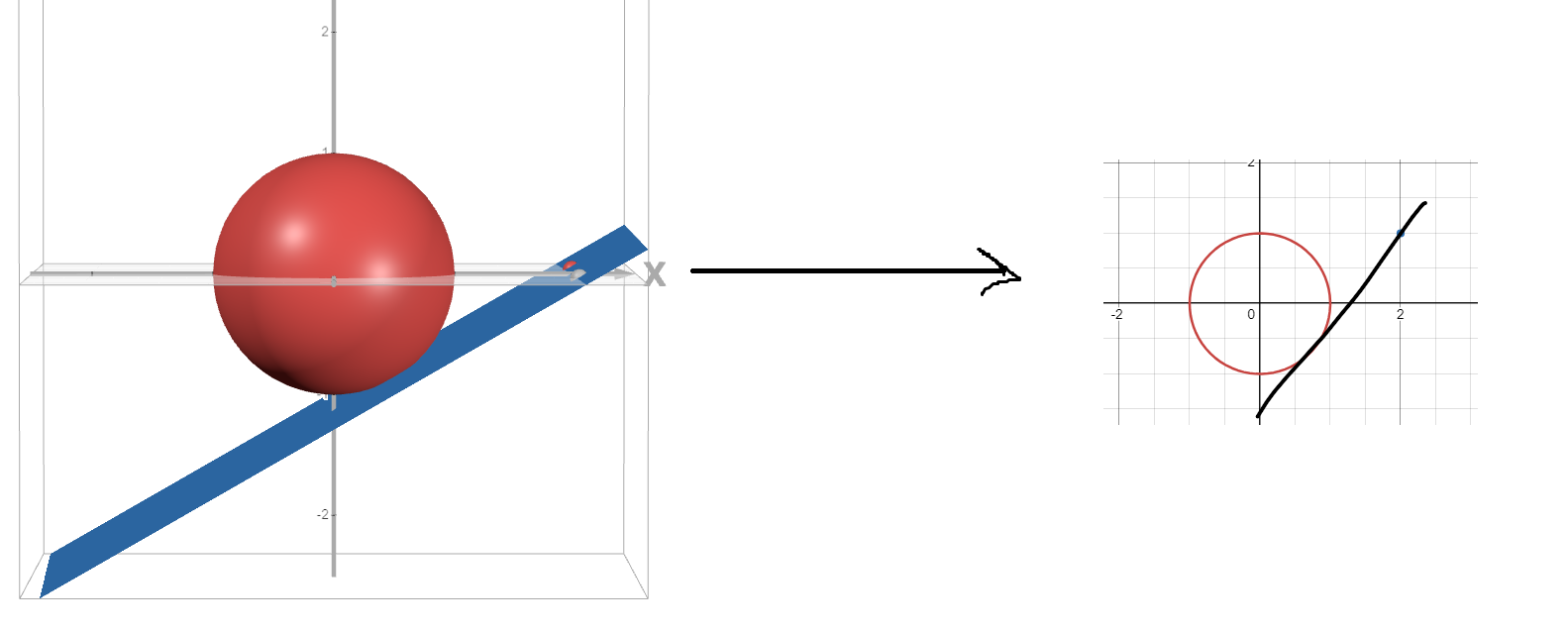
Där tangeringspunkten i 3D-fallet är och i 2D-fallet ?
Klockrent!
Tillägg: 22 okt 2024 17:27
På 2D grafen till höger borde linjen korsa punkten (2,0) dock :)
Om jag skulle vilja ta fram linjen då för att hitta tangeringspunkten, då har jag ju följande krav:
Är det smidigaste sättet då att skriva om i termer av och och sedan lösa ekvationssystemet:
?
Smaksak.
Jag skulle förmodligen kvadrera andra ekvationen och få och därefter fortsätta lösa ut x.
Okej. Och sedan när man har och så kommer man se ur ekvationerna med tre variabler att nödvändigtvis måste vara 0?
Så man hade kunnat göra exakt samma sak med att tänka bort -axeln, även om sfären definierades av , men då hade man när man går tillbaka till de fullständiga ekvationerna fått fram att istället.
Förstår jag det rätt då?
naytte skrev:Okej. Och sedan när man har och så kommer man se ur ekvationerna med tre variabler att nödvändigtvis måste vara 0?
Precis, det leder ju till y0=0. Men jag tror inte det här visar någonting eftersom att vi redan antagit att y0=0. Så skulle vårt antagande vara fel lär vi inte märka det ur detta.
Så man hade kunnat göra exakt samma sak med att tänka bort -axeln, även om sfären definierades av , men då hade man när man går tillbaka till de fullständiga ekvationerna fått fram att istället.
Förstår jag det rätt då?
Ja precis, men återigen har vi här antagit att y0=1 så det är samma situation som ovan.
Min tanke med det exemplet var helt enkelt att vi ser symmetrin i y=1 planet och därefter fortsätter i 2D fallet.
Men jag tror inte det här visar någonting eftersom att vi redan antagit att y0=0. Så skulle vårt antagande vara fel lär vi inte märka det ur detta.
Jag måste återkomma när jag har smält det här lite. Jag befinner mig tydligen fortfarande i stadiet att det inte är trivialt än. Det kommer säkerligen kännas helt uppenbart om någon eller några nätter. Jag får nog försöka hålla mig till det algebraiska helt enkelt.
Tack så mycket till er båda för all hjälp!
D4NIEL skrev:Vill man lösa det här mer "algebraiskt" kan man tänka så här; vi har tre punkter , samt . Eftersom tangeringspunkten ligger på enhetssfären kan också betraktas som en normal till tangentplanet med längden . Det ger oss följande ekvationer
(1) Varje vektor i planet ska vara vinkelrät mot normalen
(2) Varje vektor i planet ska vara vinkelrät mot normalen.
Eftersom ger ekvation (1) och (2) systemet
Som har lösningarna
Normeringsvillkoret ger sedan två möjliga värden på .
Jag har en fråga till om den här lösningen. När vi använder skalärproduktens distributiva egenskap, får vi i ekvation (1):
Men egentligen är ju en punkt och inte en vektor. Eller tänker vi att vi bildar vektorn genom att ta , där är origo? Och det kan man göra med alla punkter i rummet, så egentligen kan man betrakta alla punkter som vektorer?
Tillägg: 23 okt 2024 19:56
Och hur vet vi att "radievektorn" kommer vara en normal till planet? Kan man använda gradienter på något sätt för att visa detta? "Gradienten" som operator är ganska ny för mig men det känns som man borde kunna använda den här. Typ visa att radievektorn måste vara proportionell mot vektorn som ges av gradienten.
I väntan på D4NIEL kan jag bidra med mitt.
naytte skrev:D4NIEL skrev:Vill man lösa det här mer "algebraiskt" kan man tänka så här; vi har tre punkter , samt . Eftersom tangeringspunkten ligger på enhetssfären kan också betraktas som en normal till tangentplanet med längden . Det ger oss följande ekvationer
(1) Varje vektor i planet ska vara vinkelrät mot normalen
(2) Varje vektor i planet ska vara vinkelrät mot normalen.
Eftersom ger ekvation (1) och (2) systemet
Som har lösningarna
Normeringsvillkoret ger sedan två möjliga värden på .
Jag har en fråga till om den här lösningen. När vi använder skalärproduktens distributiva egenskap, får vi i ekvation (1):
Men egentligen är ju en punkt och inte en vektor. Eller tänker vi att vi bildar vektorn genom att ta , där är origo? Och det kan man göra med alla punkter i rummet, så egentligen kan man betrakta alla punkter som vektorer?
Precis, varje punkt kan uttryckas som den ortsvektor som går från origo till denna punkt. Varför detta kan skapa problem låter jag D4NIEL svara på.
Tillägg: 23 okt 2024 19:56
Och hur vet vi att "radievektorn" kommer vara en normal till planet? Kan man använda gradienter på något sätt för att visa detta? "Gradienten" som operator är ganska ny för mig men det känns som man borde kunna använda den här. Typ visa att radievektorn måste vara proportionell mot vektorn som ges av gradienten.
Planet skulle tangera sfären, och därmed har planet och sfären samma gradient i den punkten.
För en sfär med centrum i origo kommer alla ortsvektorer till punkter på sfären vara normalvektorer till ytan. Detta är en mycket trevlig egenskap som du kommer stöta på flera gånger.
Planet skulle tangera sfären, och därmed har planet och sfären samma gradient i den punkten.
Hur skulle man kunna skriva upp det mer "formellt"? Jag vet att om man tar gradienten av en funktion som beror på t.ex. så får man en vektor:
Men i vårt fall med sfären så har vi ju inte en funktion utan snarare en ekvation () . Hur uttrycker man gradienten då?
Sfären kan beskrivas med ekvationen . Dess gradient i en godtycklig punkt blir därmed . Normerar vi denna får vi normalvektorn .
I sfäriska koordinater får vi att gradienten är och normerade normalvektorn är
Tillägg: 23 okt 2024 22:52
Värdet på i ekvationen spelar ingen roll eftersom att denna inte förändrar gradienten, denna medför bara en parallellförflyttning i rummet.
Jämför med derivering av en konstant.
EDIT: Parallellförflyttning är fel ord. Det sker någon form av omskalning (i detta exempel kommer sfären ha radien sqrt(k), vilket innebär en sfärisk omskalning).
Så när vi tar fram gradienten så använder vi inte operatorn på "båda sidor" av ekvationen eller något sådant, utan vi utför bara operationen:
?
Bra poäng.
Det är nog funktioner vi opererar på snarare än ekvationer. I synnerhet är det oftast på vektorfält vi bestämmer gradienten.
Funktionen med är ett vektorfält som som sträcker sig från origo och utåt i alla riktningar. Ekvationen beskriver ett nivåplan i detta vektorfält, dvs ett plan i vilket funktionen är konstant. Gradienten av denna funktion beskriver sedan i vilken riktning vektorfältet växer snabbast. Det följer att gradienten alltid är ortogonal mot nivåplanet i varje punkt.
Lite halvtaskig förklaring, men allt detta kommer klarna så småningom.
naytte skrev:Jag har en fråga till om den här lösningen. När vi använder skalärproduktens distributiva egenskap, får vi i ekvation (1):
Men egentligen är ju en punkt och inte en vektor. Eller tänker vi att vi bildar vektorn genom att ta , där är origo? Och det kan man göra med alla punkter i rummet, så egentligen kan man betrakta alla punkter som vektorer?
Japp, exakt så. Lägesvektorn för blir . Och för det mesta kan man behandla punkter i rummet som vektorer. Men tekniskt sett är en punkt i rummet knuten till ett origo, eller mer egentligt knuten till själva rummet och dess egenskaper. Det innebär att du har ett helt nytt matematiskt objekt som består av två saker; en vektor och en "förankringspunkt" , t.ex. origo. För det nya objektet gäller bland annat att (jmfr med en vektor)
Men det nya objektet (som vi kan kalla tangentvektorn vid punkten ) följer inte riktigt samma regler som en vanlig vektor. Vi får till exempel INTE bilda om .
Det kan alltså vara värt att tänka på att en vektor egentligen inte har en start och en slutpunkt i "rummet" utan bara en längd och en riktning. Men det är så praktiskt och bekvämt att se punkter i rummet som vektorer att de flesta glömmer bort skillnaden.
Problem uppstår när rummets egenskaper ändras, eller när man translaterar sitt koordinatsystem. Motsatt problem uppstår när studenten behandlar vektorer som punkter i rummet som inte får flyttas.



