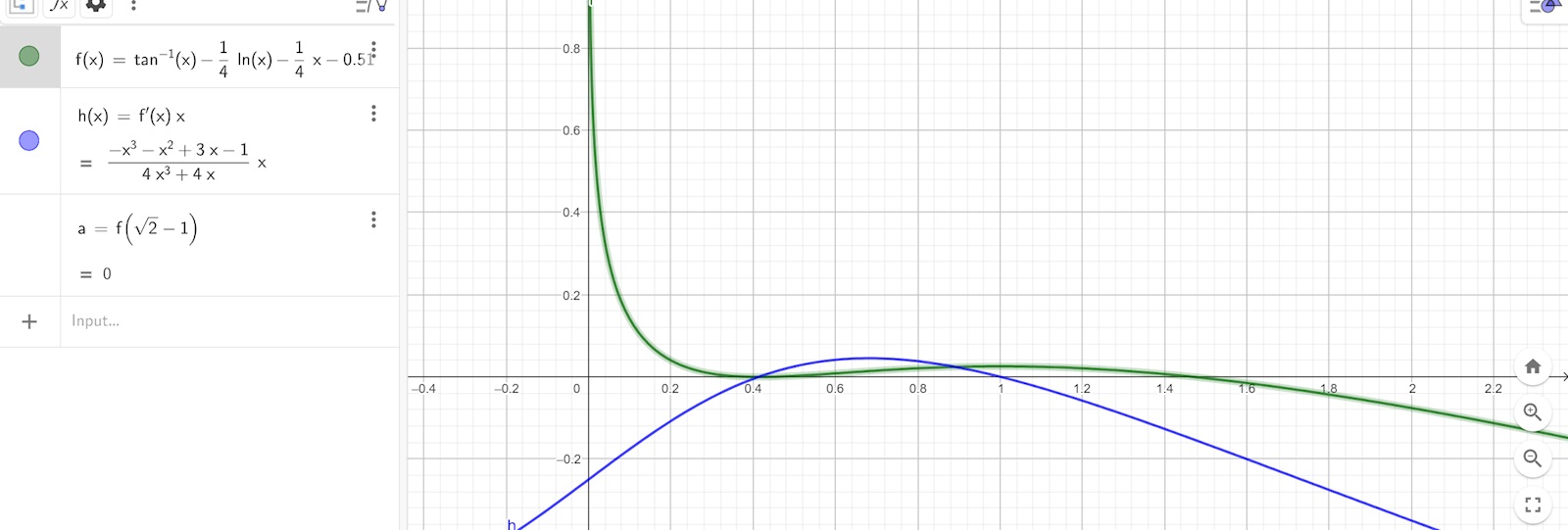
bestäma funktionen värde i en punkt

Hur kan jag så fram ett exakt värde för
Varför vill du sätta in sqrt(2)-1? Detta kommer vara den minsta värdet i det växande intervallet du har angivit. Dvs det finns med säkerhet andra punkter som kommer ge ett högre värde på a.
Calle_K skrev:Varför vill du sätta in sqrt(2)-1? Detta kommer vara den minsta värdet i det växande intervallet du har angivit. Dvs det finns med säkerhet andra punkter som kommer ge ett högre värde på a.
Då a=f(sqrt(2)-1) cirka 0.51 har jag kommit fram är den punkt där funktionen har två nollställnen. Då man har a mindre än 0.51 få jag att funktionen har ett nollställe
Testa att öka a ännu mer, hur många nollställen får du?
Calle_K skrev:Testa att öka a ännu mer, hur många nollställen får du?
Då fick jag två nollställen grafen puttades när. Så när jag minskade a alltså har det mindre än 0.51 då har jag ett nollställe.
Öka a ännu mer.
Calle_K skrev:Öka a ännu mer.
Ahhh, om jag ökar den ännu mer så har den inga nollställen. Jag vet dock fortfarnde inte vad jag ska svara
Sista termen är ju -a, så om du ökar a mer (dvs minskar sista termen) får du ett nollställe igen.
Calle_K skrev:Sista termen är ju -a, så om du ökar a mer (dvs minskar sista termen) får du ett nollställe igen.
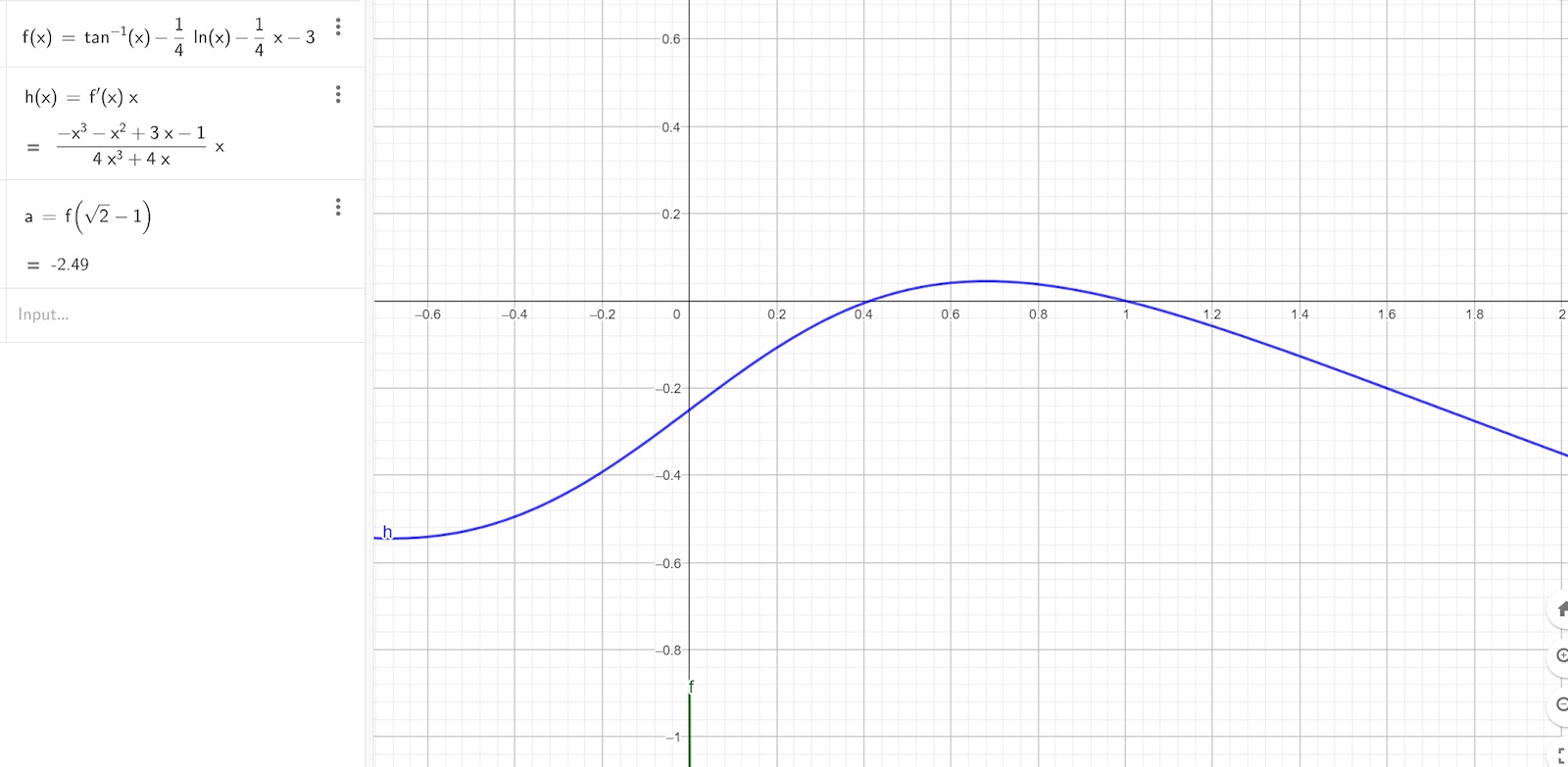
Jag tolkade det som att hela grafen hamnde under x-axeln. Men det är så att grafen forstätter genom x-axeln trots att jag inte kan se det på grafritaren?
Varför undersöker du den grafen? Och inte f?
Calle_K skrev:Varför undersöker du den grafen? Och inte f?
du ser f grafen längre ner i bilden
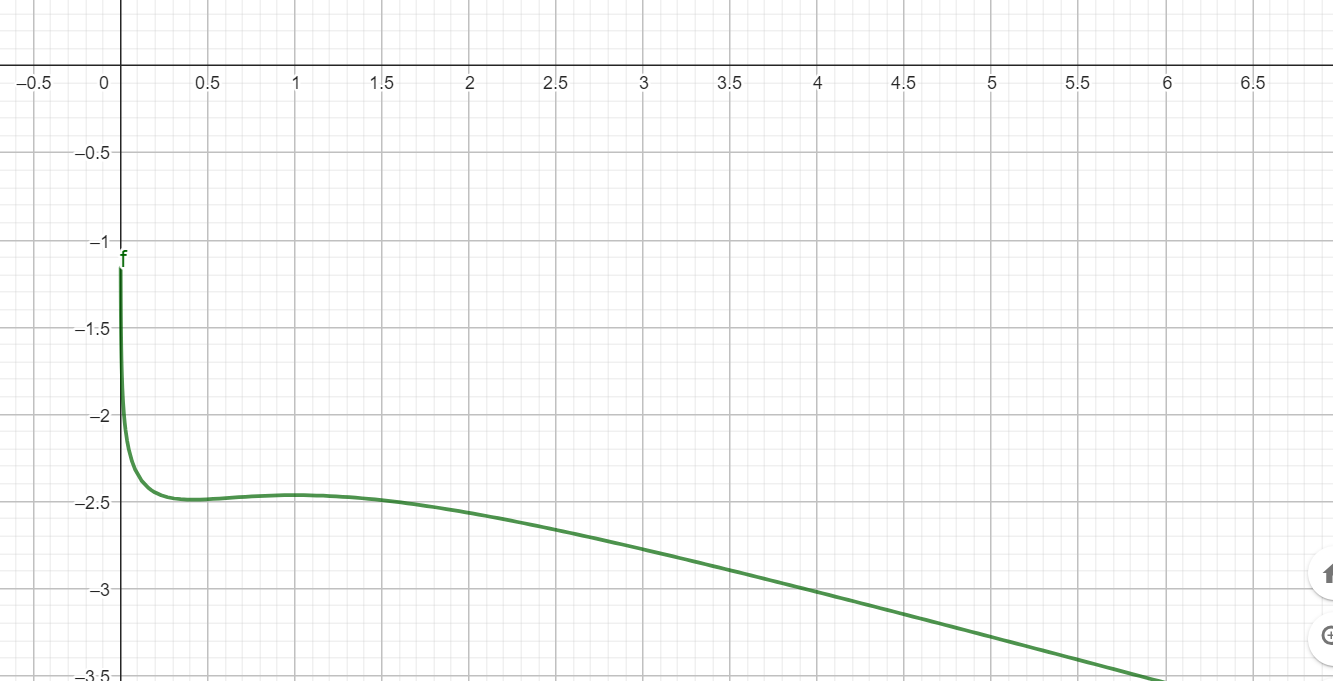
Ok, lite svårt att se i den grafen men värdet kommer fortsätta mot oändligheten.
Stoppa in x=0 i ekvationen, vad får du?
Calle_K skrev:Ok, lite svårt att se i den grafen men värdet kommer fortsätta mot oändligheten.
Stoppa in x=0 i ekvationen, vad får du?
Ahhh okej, nu ser jag. Eftersom att ln0 inte är definerad kommer därför därför att funktionen att på mot positivoändlighet då x går mot noll.
Philip22 skrev:Calle_K skrev:Ok, lite svårt att se i den grafen men värdet kommer fortsätta mot oändligheten.
Stoppa in x=0 i ekvationen, vad får du?
Ahhh okej, nu ser jag. Eftersom att ln0 inte är definerad kommer därför därför att funktionen att på mot positivoändlighet då x går mot noll.
Okej nu sluten förstår jag, tog sin lilla tid. Eftersom att funktionen fortsätter mot positiv oändlighet så kommer där a ha minst en lösningen till att värden på a.
Tack för hjälpen Calle! :D
Toppen!