Bestäm x till ekvationen:

$E k v a t i o n e n : a r c \sin x = a r c \cos 2 x e n l i g t f o r m e \ln : a r c s \sin x + a r c \cos x = \frac{π}{2} d å a r c \sin x = \frac{π}{2} - a r c \cos x \frac{π}{2} - a r c \cos x = a r c \cos 2 x, a r c \cos x = u \frac{π}{2} = 3 u, u = \frac{π}{6}, a r c \cos x = \frac{π}{6}, x = \cos \frac{π}{6} = \frac{\sqrt{3}}{2} e n l i g t f a c i r ä r x = \frac{1}{\sqrt{5}}, H u r ?$

Tips: rita en rätvinklig triangel med kateterna $x$ resp. $2x$ och hypotenusan $1$ .

Jag känner inte igen formeln du använt. Det vanligaste sättet att lösa denna typ av uppgifter på är nog att först förenkla ena ledet:

$\sin (\arcsin (x)) = \sin (\arccos (2 x)) x = \sin (\arccos (2 x))$

Nu kan vi rita lite! Vi vill rita en triangel där en sida kan skrivas som arccosinus av 2x. Det första vi behöver göra är därför att sätta ut en sida som är 2x:

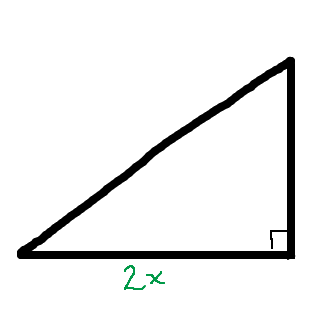
Om nu en vinkel ska kunna vara arccosinus av 2x, behöver vi se till att hypotenusan är ett, så att den närliggande vinkeln verkligen kan skrivas som $\arccos (2 x) = \arccos (\frac{2 x}{1})$ . Vi sätter därför hypotenusan till ett, och vinkeln blir då arccos(2x):

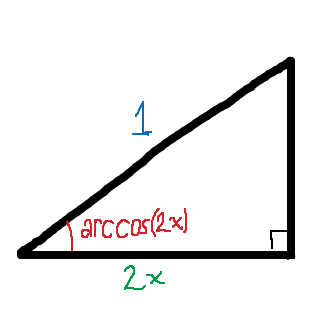
Nu kan vi med hjälp av pythagoras sats beräkna den motstående kateten (den lodräta) till $\sqrt{1^{2} - {(2 x)}^{2}} = \sqrt{1 - 4 x^{2}}$ . Vi sätter in det i vår triangel:

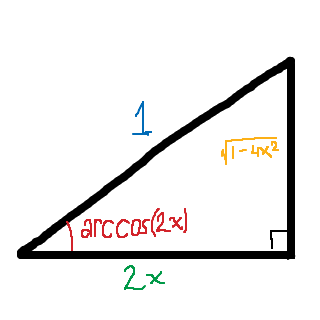
Vi kan nu beräkna $\sin (\arccos (2 x))$ , genom att helt enkelt beräkna sinusvärdet av vinkeln som heter arccos(2x). Vi får då att $x = \sin (\arccos (2 x)) = \frac{\sqrt{1 - 4 x^{2}}}{1} = \sqrt{1 - 4 x^{2}}$ .

Ekvationen $x = \sqrt{1 - 4 x^{2}}$ kan lösas på vanligt sätt – kvadrera båda led, och lös ut x. :)

Om funktionen y=sin(a) har tal som y värde så har funktionen z=arcsin(b) vinklar som z-värden.

En tolkning av arcsin(x)=arccos(2x) är skärningspunkten mellan funktionerna y1=arcsin(x) och y2=arccos(2x). En snabb skiss av dessa funktioner visar att det finns bara 1 skärningspunkt. I skärningspunkten så har funktionerna samma y värde, kalla denna vinkel a. Från skissen kan vi även konstatera att a ligger i första kvadranten.

a=arcsin(x)
sin(a)=x

a=arccos(2x)
cos(a)=2x

Med sin(a) och cos(a) kan vi nu rita en triangel i 1:a kvadranten i enhetscirkeln.

${(2 x)}^{2} + {(x)}^{2} = 1 5 x^{2} = 1 x = \frac{1}{\sqrt{5}}$

Den negativa roten ignoreras eftersom a ska vara i 1:a kvadranten.

Svara

Visa senaste svar