Bestäm uttrycket för cirkelns area
Bestäm uttrycket som ger möjlighet att kunna beräkna cirkelns area då cirkelns mitt är placerat i origo och punkten P ligger på cirkelperiferin.
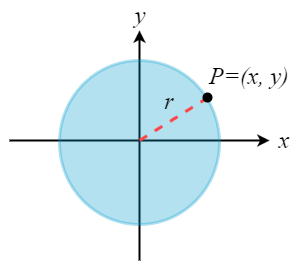
Min första tanke är att använda Pythagoras sats för att bestämma y eftersom att det kommer att ge formeln för hela arean i det första området (Skriv gärna ifall det är fel tankesätt) vilket ger y^2=sqrt(r^2-x^2). Integrations gränserna blir 0 och r för ifall hela området ska täckas måste den börja med noll och sluta vid r i x-axeln. Arean blir endast för området i den första kvadranten och därför multiplicerar jag integralen med 4. Integralen blir . Fast är lite osäker på ifall mitt tankesätt för de olika processerna är korrekta samt även lösningen och detta var en uppgift jag hitta på nätet utan facit
Hej!
Tankesättet är korrekt, men blir något svår att hitta primitivfunktion. Ett sätt för att förenkla det är att göra en variabelsubstitution, vilket jag antar ni inte har gjort ännu i kursen?
Ett alternativt sätt för att bestämma arean hos en cirkel är att utnyttja att vi vet hur cirkelns omkrets är definierad dvs samt delar in cirkeln i små segment som på bilden. (Säg till ifall du vill ha en förklaring)

Sätt
Fast stämmer uttrycket för uppgiften handlande endast om att bestämma uttrycket för arean
Fotbollskillen12 skrev:Fast stämmer uttrycket för uppgiften handlande endast om att bestämma uttrycket för arean
Du kan testa integrera
Förhoppningsvis ska arean på cirkeln trilla ut.
.jpg?width=800&upscale=false) Uppgiften hade följande alternativ, var dock osäker kring tankesättet för de olika värden
Uppgiften hade följande alternativ, var dock osäker kring tankesättet för de olika värden
Fotbollskillen12 skrev:
Uppgiften hade följande alternativ, var dock osäker kring tankesättet för de olika värden
Okej, läste inte din fråga ordentligt!
Utifrån de alternativ som finns där så är det sista alternativet passande för att bestämma uttrycket för cirkelns area. Varför du använder pythagoras sats är för att vill du ta fram en funktion för y = f(x) som beror på variabeln x i detta fallet
Vid multiplikation med 4 gör du för att varje kvadrant har samma form (pga cirkel).
Fast vad hade hänt om man endast hade haft r? Varför vill man få fram y
Fotbollskillen12 skrev:Fast vad hade hänt om man endast hade haft r? Varför vill man få fram y
I detta fallet så integreras det med avseende på x. Hur du vet att det är med avseende på x utgörs av beteckningen dx i integralen.
Anledningen till att y vill bestämmas är för att du vill veta längden i höjdled. Om du kanske minns så introducerades konceptet integral först genom som en summa av arean hos ett antal staplar under en kurva, se bild nedan. Staplarnas höjd utgörs utav en kurvas funktion f(x)=y och bredd utgörs av dx. Arean för en rektangel påminner vi oss som basen x höjden och då har varje stapel arean, f(x)*dx = y*dx. - (Notera att varje stapel inte ha samma höjd. Varför?) Vid summering av varje staplar så erhålls arean under en kurva och beräknas genom,
- notera att om dx är "litet" så blir approximationen av arean också bättre då staplarna bli smalare.

Absolut så skulle man kunna integrera med avseende på y. Resultatet hade fortfarande blivit detsamma.
Så om det deriverades med avseende på y hade y varit basen då? Fast vad är r i detta fallet då?
Fotbollskillen12 skrev:Så om det deriverades med avseende på y hade y varit basen då? Fast vad är r i detta fallet då?
Så om det deriverades med avseende på y hade y varit basen då?
Jag antar att du menar integreras, men ja.
Fast vad är r i detta fallet då?
r kan ses som en konstant som ska utgöra radien hos cirkeln.
Fast har svårt att visualisera det hela hur det hade sett ut i en graf hur hade r på verkat höjden?
Fotbollskillen12 skrev:Fast har svårt att visualisera det hela hur det hade sett ut i en graf hur hade r på verkat höjden?
Antag att radien r på cirkeln är fixt. Om du drar punkten längs med cirkelns rand så kommer längden från origo till punkten på randen att ha samma längd, dvs r. Om du kan tänka dig inskrivna rätvinkliga trianglar som på bilden nedan så ser du att höjden y beror på både r och x. Men eftersom r var fixerad så är det bara x (motsvarar den andra kateten) som förändras.
 Hoppas det klargjorde något!
Hoppas det klargjorde något!


