Bestäm u(t) spole

Hej!

Hur kom du fram till villkoret i(0)=0.008A?

(Det är inte konsistent med uttrycket i punkt 4, så någonstans måste du ha gjort fel)

Jag tror du har beskrivit begynnelsevillkoret för totala strömmen, dvs såhär

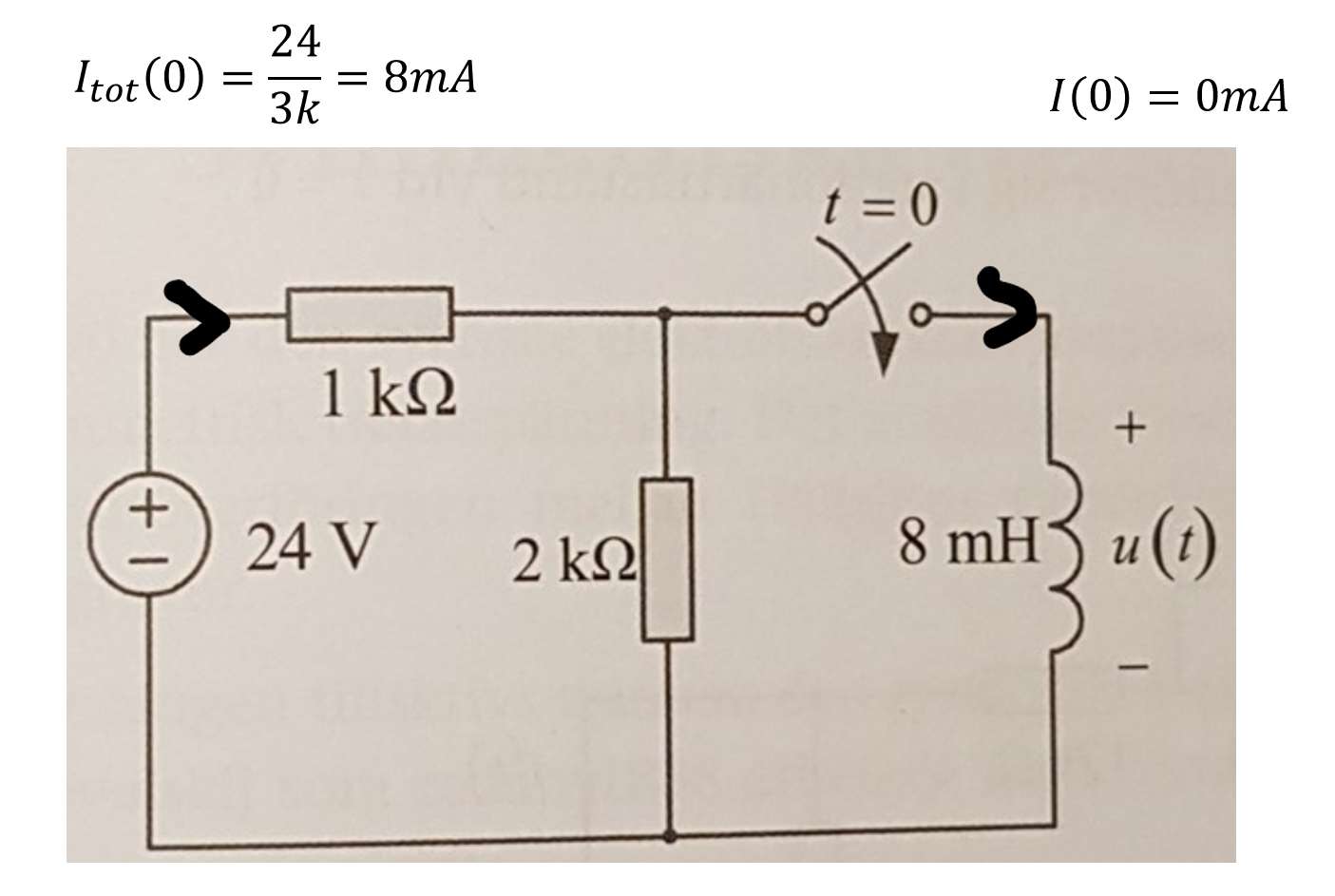
Den strömfunktion som du ska räkna ut är strömmen genom induktansen. Den är $I\left(0\right)=0$, ser du det?

Okej jag förstår, så begynnelsevillkoret ska man alltid räkna över t.ex spolen eller kondensatorn? Jag tänkte att eftersom brytaren är öppen vid i(0) så går det ingen ström där och då ska man räkna i den vänstra kretsen.

Jag förstår hur du tänker, och det är ju inte feltänkt om du vill beskriva strömmen i kretsen som innehåller batteriet. Men det som du betecknar "i" under punkt 1 och under punkt 4, är inte samma ström. Så det är lite svårt för mig att konstatera var du har tänkt fel. Du kan eventuellt av misstag bara ha använt samma beteckning "i" på olika strömmar.

Sätter du in t=0 i strömfunktionen undre punkt 4 så får du i(0)=0, vilket stämmer. Så frågan är vilket begynnellsevilkor du använde när du räknade fram i(t)-funktionen i punkt4 (vilken har rätt "utseende", men fel siffror).

Kan du visa hur du gör steg3 så kan vi se var du gör fel, för om du väl kommer till steg4 med en riktig strömfunktion så kan du sedan beräkna spänningen över spolen med $u=L\frac{di}{dt}$ 

Jag får fram rätt svar 16e^-83333t när jag använder mig av ditt tänk att i(0)=0 för då får jag i(t)=-0.024e^-83333t+0.024. Men jag är lite osäker hur man ska det här med begynnelsevillkoret, vad som är rätt/fel och över vad man räknar det. 

Det där kom jag också fram till, och det tror jag stämmer, bra!

Du ska tänka att när induktansen kopplas in vid t=0 och strömmen ska börja flyta genom den, så ser den ut som en öppen krets (induktansen vill motverka strömförändringar).

Jag tror att det som förvirrar dig med begynnelsevillkoret du beskriver i steg1 är att det är en annan ström än den som flyter genom spolen. Strömmen som du beskriver i steg1 är före du har gjort om kretsen till tvåpolsekvivalent, finns inte längre i tvåpolsekvivalenten. Du måste ha begynnelsevilkoret för den ström som flyter genom spolen, vilket är strömmen i tvåpolsekvivalenten.

Nu blev jag lite mer förvirrad.. enligt din logik så kommer strömmen i tvåpolsekvivalenten vara 0, detta stämmer inte? Enligt detta påstående:

Strömmen som du beskriver i steg1 är före du har gjort om kretsen till tvåpolsekvivalent, finns inte längre i tvåpolsekvivalenten. Du måste ha begynnelsevilkoret för den ström som flyter genom spolen, vilket är strömmen i tvåpolsekvivalenten.

Det jag menar är att du kan inte räkna med ett begynnelsevillkor på strömmen i ursprungskretsen, eftersom det är inte den ström som går genom induktansen (begynnelsvilkoret på denna ström är 8mA vid t=0).

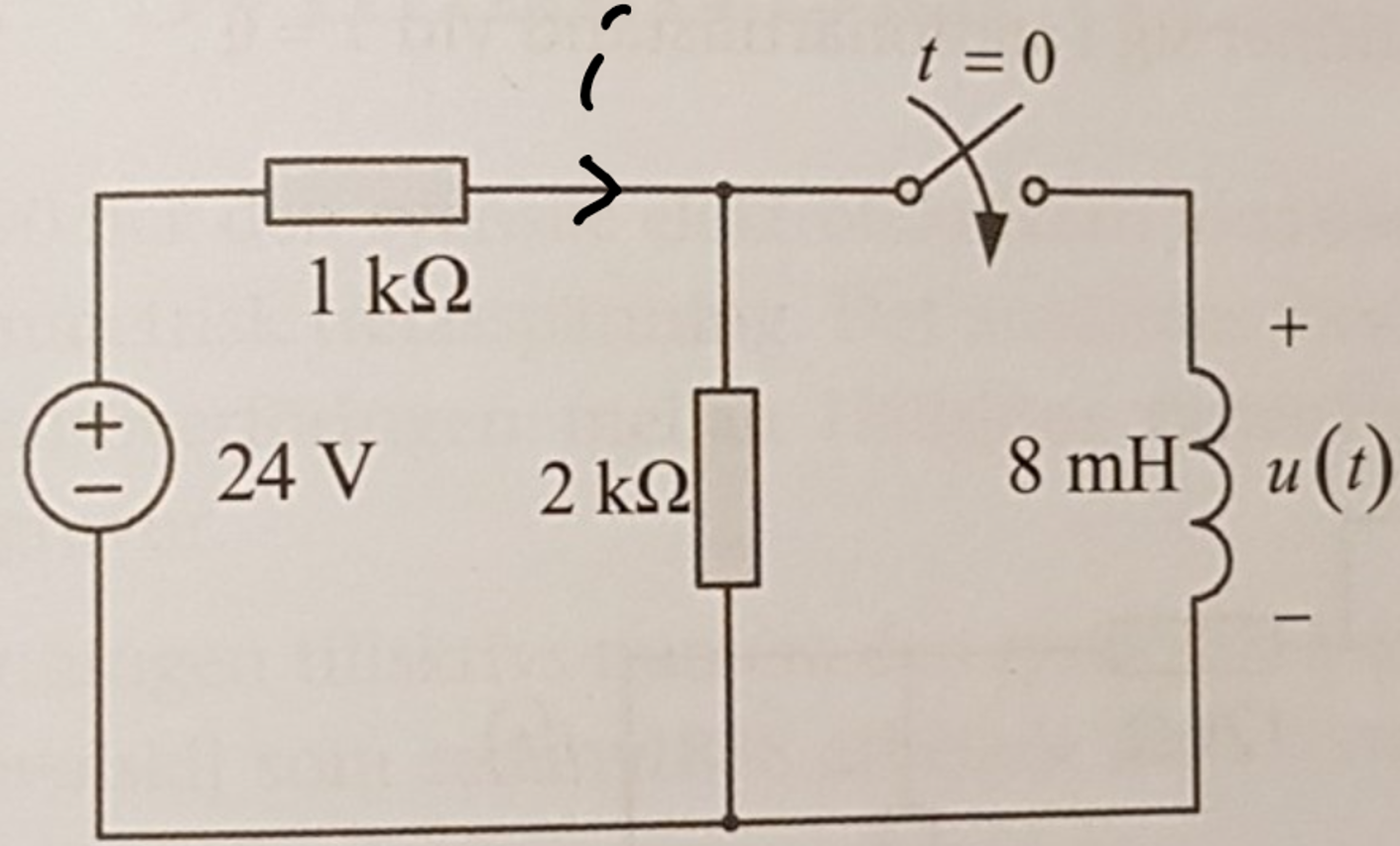
Utan du måste ha ett begynnelsevillkor på strömmen i tvåpolsekvivalenten, som går genom induktansen (begynnelsvilkoret på denna ström är 0mA vid t=0):

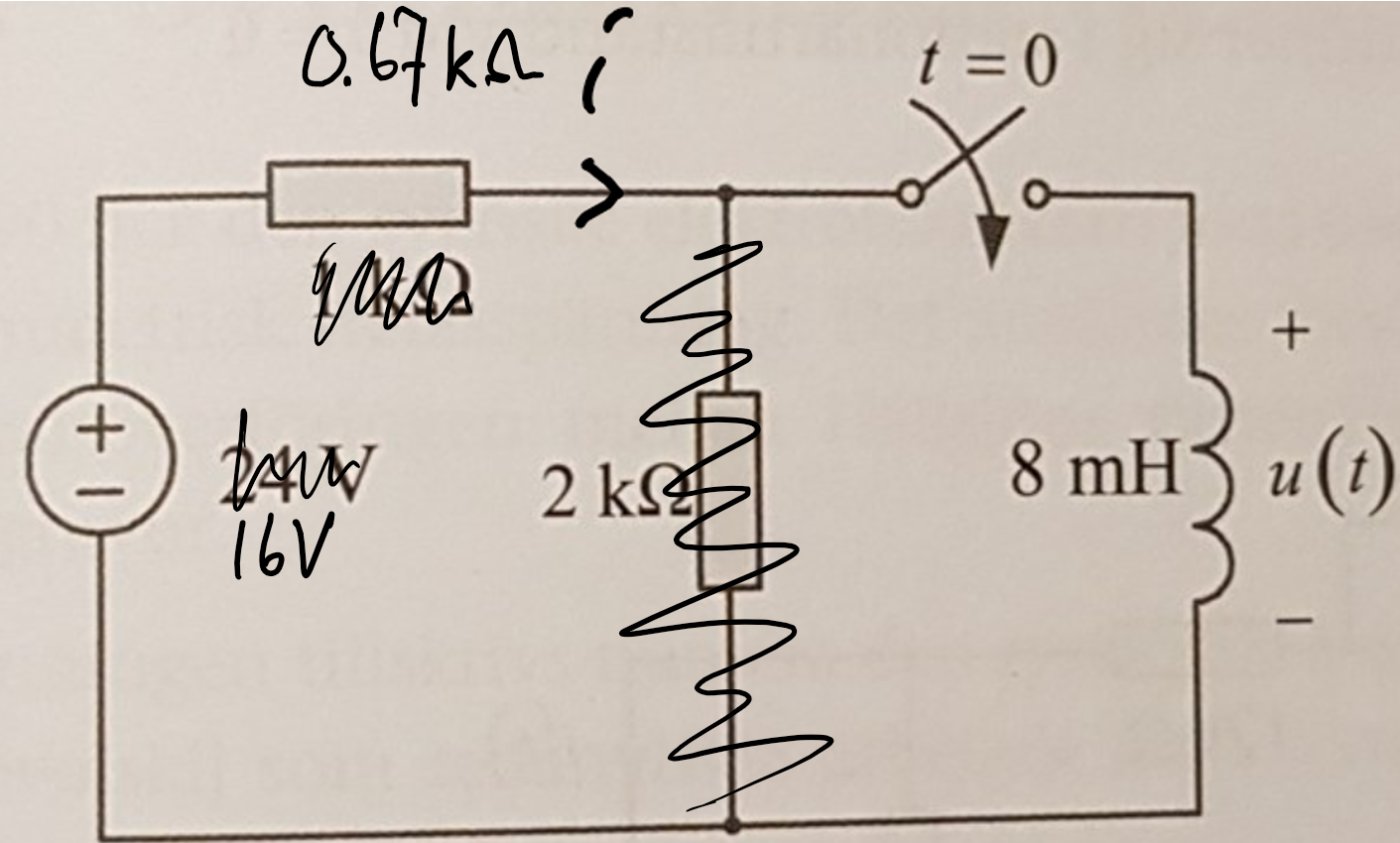
Hänger du med?

Jag testade det och det ger inte i(0) = 0 så hur ska det vara begynnelsevillkoret?

Jag testade det

Vad för någonting testade du? Jag hänger inte riktigt med på vad du menar med "det".

Såhär gjorde jag:

-KVL runt den förenklade kretsen ger den inhomogena diffekvationen av första ordningen

$$\begin{gathered} 16-667·i-0.008·\frac{di}{dt}=0 \Rightarrow \\ i+1.2·{10}^{-5}·\frac{di}{dt}=0.024 \end{gathered}$$

Vilket ger partikulärlösningen $i_p=0.024$ och allmänna lösningen till motsvarande homogen diffekvation $i_h=C·e^{-\frac{t}{1.2·{10}^{-5}}}$

Alltså, den allmänna lösningen till den inhomogena diffekvationen blir

$i\left(t\right)=C·e^{-\frac{t}{1.2·{10}^{-5}}} + 0.024$

Eftersom begynnesevillkoret är att strömmen genom induktansen är 0 vid t=0, dvs $i\left(0\right)=0$, så ger det $C=-0.024$

Det betyder att strömmen genom induktansen beskrivs av funktionen

$i\left(t\right)= 0.024·\left(1-e^{-\frac{t}{1.2·{10}^{-5}}}\right)$och spänningen över induktansen blir därför

$u\left(t\right)=L·\frac{di}{dt}=0.008·0.024·\frac{1}{1.2·{10}^{-5}}·e^{-\frac{t}{1.2·{10}^{-5}}}=16·e^{-\frac{t}{1.2·{10}^{-5}}}$

Hur gjorde du?

Jag gjorde exakt så men jag förstår inte ditt uttryck om att "du måste ha ett begynnelsevillkor på strömmen i tvåpolsekvivalenten, som går genom induktansen" det är väl exakt samma som om man inte hade omvandlat till tvåpolen för, som du konstaterade är det strömmen genom spolen som ger begynnelsevillkoret, vilket är 0 båda fallen. 

Jag vet inte om vi kanske pratar förbi varandra? Det jag menar är att strömmen som jag betecknar som "i" i första fig inlögg#9 har i(0)=8mA, och är _inte_ den ström som går genom induktorn. Jag misstänkte att det var denna ström som du räknade ut och redovisade i steg1 i ts, men jag kan ha fel. Däremot är strömmen genom induktorn såklart 0mA vid t=0 även i den icke-förenklade kretsen. Du hade ju lika gärna kunnat lösa uppgiften utan att först förenkla kretsen, men då varit tvungen att räkna ut de olika nodströmmarna med KCL istället, för att se vilken ström som går genom induktorn och ställa upp en diffekvation för just den strömmen.

Är du med på vad jag menar? 

Ja jag tror vi pratade förbi lite haha, men jag är med nu!

Va bra!