Bestäm tangentens ekvation 2
Grafen till har en tangent i punkten (-1,3)- Bestäm tangentens ekvation.
Jag gjorde så här:
Ändrade rubriken så att den går att urskilja från tråden innan denna. Snälla använd mer beskrivande titlar, eller numrera dem åtminstone! /naytte
Det ser bra ut! Är det något du undrar över?
nja, i facit står det att svaret är y=-6x-3
Du missar ett minustecken på ett ställe.
Försök gärna att hitta felet själv, kanske med den metod jag föreslog i din andra tråd.
Om du inte hittar det så beror det nog på att du tar för stora tankekesteg/räknesteg åt gången.
Skriv ut alla mellanresultat på separata rader.
Ett annat fel (som inte påverkar uträkningen) är att du glömmer att skriva efter detta likhetstecken:

Jag får dessvärre samma fel igen

Du har rätt i att f'(x) = 6x (men du glömde återigen att skriva ut på ett ställe).
Du skriver att f'(-1) = 3. Det stämmer inte.
Derivatans värde i en punkt är lika med funktionsgrafens lutning I den punkten.
Om tangeringspunkten är (-1, 3) så är f'(-1) alltså lika med lutningen på den tangent som tangerar kurvan vid (-1, 3).
=====
Använd gärna Desmos för att skissa grafen till f(x) = 3x2
Börja med att beräkna denna lutning.
yngve jag skrev in denna på desmos men lyckades inte få något bra svar.
Har du möjlighet att göra ett lösningförslag så att jag kan härma och i framtiden lösa frågan smidigare
Arup skrev:yngve jag skrev in denna på desmos men lyckades inte få något bra svar.
Jag tänkte inte att du ska lösa uppgiften med hjälp av Desmos, bara att du ska se hur parabeln ser ut och därigenom dels få lite inspiration till hur du kan gå tillväga för att lösa uppgiften, dels ha som stöd i en rimlighetskontroll när du får fram ett svar.
Har du möjlighet att göra ett lösningförslag så att jag kan härma och i framtiden lösa frågan smidigare
Jag kan ge dig förslag på de steg du kan gå igenom I din egen lösning:
- Rita en skiss över grafen till y = f(x).
- Om du ritar för hand, skissa grovt en tangent enligt uppgiftslydelsen
- Ta fram ett uttryck för f'(x).
- Beräkna med hjälp av f'(x) tangentens lutning, dvs k-värdet i tangentens ekvation y = kx+m.
- Använd det faktum att den givna punktennligger på tangenten för att bestämma m-värdet i tangentens ekvation y = kx+m.
- Kontrolleramed hjälp av din skiss att svaret verkar rimligt.
- Klart.
Säg till om det är något/några av dessa steg som du inte förstår eller som du är osäker på hur du ska utföra.
=======
Du tänkte alltså rätt hela vägen, men du fick fram fel värde på k..
yngve jag gjorde följde ju alla steg
Arup skrev:yngve jag gjorde följde ju alla steg
Nej, jag kan inte se att du har gjort steg 1, att rita en skiss. Det är ett väldigt viktigt steg - det hjälper en att se om lösningen är rimlig (inte om den är rätt).
Arup skrev:yngve jag gjorde följde ju alla steg
Steg 1 och steg 2: Har du inte gjort.
Steg 3: Här fick du fram rätt resultat (men skrev lite fel på vägen).
Steg 4: Jag ser inte att du har gjort det. Om du menar att det är raden där det står f'(-1) = 3 så är det fel. Du använder senare att k-värdet är 6, men du visar inte hur du kom fram till det (och det är inte heller rätt).
Steg 5: Detta har du gjort, men du fick fram fel m-värde eftersom du räknade med ett felaktigt k-värde från steg 4.
Steg 6: Har du inte gjort (eftersom du inte hade någon skiss).
======
Jag rekommenderar att du
- gör steg 1 och 2 och att du visar oss hur det ser ut.
- gör steg 4 med utförlig beskrivning av hur du gör
- gör om steg 5 med ett korrekt k-värde
- gör steg 6 och berättar för oss vad du kommer fram till
Kommentar på att du fick fram k-värdet 6:
Troligtvis har du gjort det klassiska misstaget att räkna i huvudet utan att skriva ner uträkningarna.
Det är olämpligt eftersom det
- ökar risken för felräkning och
- minskar möjligheten för dig att själv kontrollera uträkningarna i efterskott.
Varför blir det svårare för dig att då kontrollera i efterskott?
Jo, eftersom uträkningen inte finns på papper utan endast fanns i ditt huvud när du skrev det första gången så blir det svårt för dig att följa exakt samma tankegång i efterskott.
Då blir det lätt så att du tänker "Jag tänkte nog rätt när jag skrev det" och du hittar då inte eventuellt räknefel.
varför ska det vara så svårt ?
Arup skrev:varför ska det vara så svårt ?
För att du tar för stora steg och inte är tillräckligt systematisk. Om du fäljer de tips du har fått av Yngve kommer det att gå mycket bättre.
Arup skrev:varför ska det vara så svårt ?
Det viktigaste felet du gör är att du inte beräknar derivatans värde vid tangeringspunkten.
Du behöver veta det eftersom detta är lika med tangentens lutning, dvs tangentens k-värde.
Eftersom tangeringspunkten är vid (-1, 3) så är derivatans värde där lika med f'(-1).
Beräkna nu detta värde aå går vi vidare sen.
Eller vad menar du med svårt?
Vilken/vilka delar tycker du är svåra?
- Är det begreppen som används (tangent, tangeringspunkt, derivata, lutning, k-värde, m-värde mm)?
- Är det hur begreppen hänger ihop (en tangent har samma lutning som funktionsderivatans värde i tangeringspunkkten, tangeringspunkten är gemensam med funktionsgrafen och tangenten osv)?
- Är det att förstå eller utföra mina föreslagna steg 1-6?
- Eller något annat?
Du kanske har fått så många tips här att du har blivit förvirrad. Om något, så ta vara på denna:
Yngve skrev:
Det viktigaste felet du gör är att du inte beräknar derivatans värde vid tangeringspunkten.
Du har nämligen, helt korrekt, kommit fram till att derivatan ser ut så här:
Arup skrev:
f'(x)=...=6x
Sen blir det lite fel/oklart, och du lurar dig själv tror jag, när du skriver att k=6x.
Steget efter f'(x)=6x är att kolla vad derivatan är för x=-1 (tangeringspunkten), precis som Yngve säger.
I övrigt kan jag bara stämma in i kören, att en figur hjälper mycket och minskar felrisken och gör rimlighetskontroll av svaret enklare.
Så i punkten (-1,3) är x=-1 och derivatan f´(-1)=6*(-1= = -6
Räta linjens ekvation är y=kx+mEftersom k=-6 i detta fall, så kan vi uttrycka räta linjens ekvation somy=-6x+mEftersom tangenten går genom punkten (-1,3), så ger det:3=-6*(-1)+m3=6+mm=-3Tangenten genom punkten (-1,3) blir alltså -6x-3
Arup skrev:Så i punkten (-1,3) är x=-1 och derivatan f´(-1)=6*(-1= = -6
Räta linjens ekvation är y=kx+mEftersom k=-6 i detta fall, så kan vi uttrycka räta linjens ekvation somy=-6x+mEftersom tangenten går genom punkten (-1,3), så ger det:3=-6*(-1)+m3=6+mm=-3Tangenten genom punkten (-1,3) blir alltså -6x-3
Bra! Allt detta stämmer.
Är det din egen lösning eller har du kopierat den från något annat ställe?
Om du har kopierat den, hängde du med på alla steg?
Och har du lyckats rita en grov skiss av parabeln y = 3x2 med en tangent på ungefär rätt ställe?
Om ja, ser du då att du kunde använda den skissen dels till att inse att ditt första resultat y = 6x+9 måste vara fel, dels till att se att det senaste resultatet y = -6x-3 verkar rimligt?
ja jag tittade även på youtube för bättre förstålse för dessa problem
jag löste den igår faktiskt sent på kvällen, men postade dock aldrig lösningen. Var för trött
Är d2t här en bra lösning ?

Arup skrev:jag löste den igår faktiskt sent på kvällen, men postade dock aldrig lösningen. Var för trött
Jag är lite nyfiken: Vad var det som var svårt i morse (svar #15) om du löste uppgiften igår kväll?
Yngve skrev:Arup skrev:jag löste den igår faktiskt sent på kvällen, men postade dock aldrig lösningen. Var för trött
Jag är lite nyfiken: Vad var det som var svårt i morse (svar #15) om du löste uppgiften igår kväll?
jag tolkade k värdet som 6
men glömde sedan multiplicera med -1
se här :
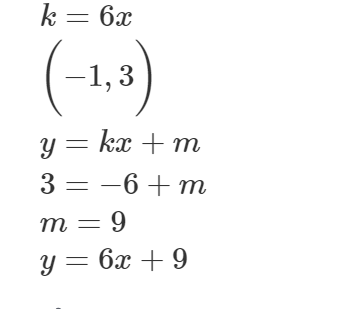
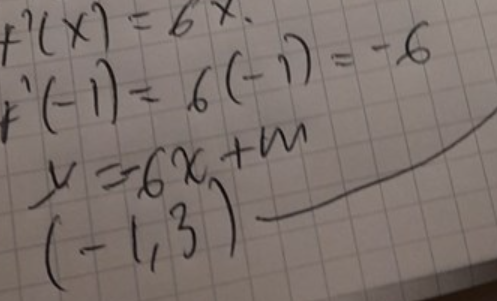
Om du hade ritat så skulle du ha sett att nånting var konstigt.
Jag förstår fortfarande inte
Om du säger att du löste den igår kväll, vad var det då som var svårt i morse?



