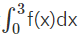Bestäm talet a, integraler

Bestäm först vad $f\left(0\right)$har för värde

Sedan bestämmer du integralen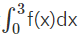

När du gjort det så sätter du det lika med värdet för f(0) och beräknar a

Tack!

Om jag fått fram att a=-3, har jag räknat rätt?

Mattemats skrev:

Bestäm först vad $f\left(0\right)$har för värde

Sedan bestämmer du integralen

När du gjort det så sätter du det lika med värdet för f(0) och beräknar a

Tack!

Om jag fått fram att a=-3, har jag räknat rätt?

Visa steg för steg hur du har räknat, så är det lättare för oss att se om du har gjort rätt.

Smaragdalena skrev:

Visa steg för steg hur du har räknat, så är det lättare för oss att se om du har gjort rätt.

f(0)=0^2+a*0+3

f(0)=3

f(3)=3^2+a*3+3

f(3)=9+3a+3

f(3)=3a+12

F(3)-F(0) = 3a+12-3 = 3a+9

3a+9=0

3a=-9

3a/3=-9/3

a=-3

Nej inte riktigt, det är ju ${\int }_0^3{x}^2+ax+3dx$som ska vara lika med $f\left(0\right)$

Mattemats skrev:

Nej inte riktigt, det är ju ${\int }_0^3{x}^2+ax+3dx$som ska vara lika med $f\left(0\right)$

Hm, trodde att det var det jag hade gjort.

Jag satt in 0 och 3 i funktionen, tog F(3)-F(0) och sen tog jag resultatet = 0. Kan inte komma på vart jag gjorde fel.

${\int }_0^3{x}^2+ax+3dx ={\left[\frac{x^3}{3}+\frac{a{x}^2}{2}+3x\right]}_0^3 = \frac{27}{3}+\frac{9a}{2}+9$