Bestäm sträcka

Hej

kan någon hjälpa mig med att förstå hur det är meningen att man ska kunna lösa följande uppgift:

En cirkel med medelpunkten O har radien 4cm. De båda tangenterna från en punkt P utanför cirkeln tangerar cirkeln i punkten S och T. Den räta linjen OP skär kordan ST i en punkt Q. Bestäm OQ om OP=12cm

När jag har ritat ser jag att vi får dels en triangel av punkterna PST och dels har vi att ST och OP skär varandra någonstans på sträckan 0-4cm.

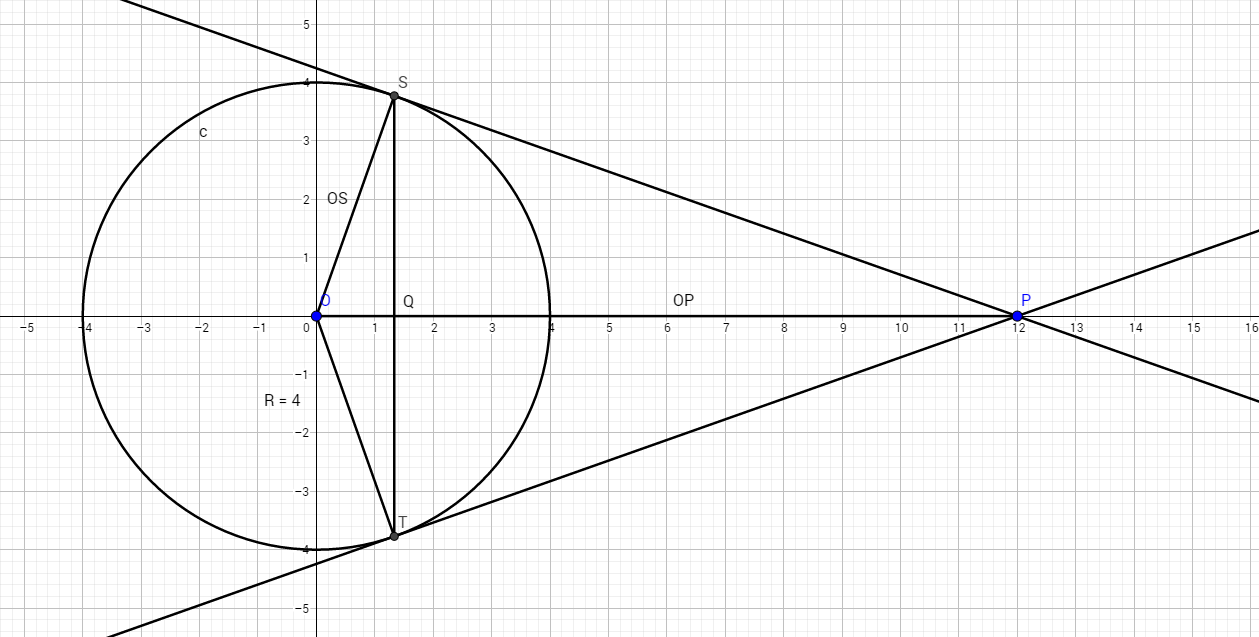
Om jag tolkat uppgiften rätt så ser situationen ut enligt ovan, jag baserar min lösning på den.

Eftersom $P S = P T$ är en tangent till cirkeln så kommer radien vara vinkelrät mot tangenterna (Bevis).

Du har nu två rätvinkliga trianglar $△ O S P ≅ △ T O P$ . $∠ O T P$ och $∠ O S P$ är $⊥$ .

Eftersom $O S = 4 c m$ och $O P = 12 c m$ har du att sträckan (från pythagoras sats) $S P = \sqrt{O P^{2} - O S^{2}} = \sqrt{128}$ . Med lite trigonometri ser du att $∠ O P S = a r c \cos (\frac{S P}{O P})$ . Nu har du att $∠ S O P = 180 - 90 - ∠ O P S$ .

Om vi kollar på $△ O S Q$ så ser du att $∠ S O Q = ∠ S O P$ .

Hitta $∠ O S Q$ med hjälp av symmetri (likbent $△ O S T$ ) om du inte kan motivera att $∠ O Q S$ är vinkelrät och på så sätt ta hjälp av $∠ S O Q$ .

När du hittat $∠ O S Q$ kan du använda dig av detta samband.

Kollar du på länken ser du att i ditt fall är $b = O Q, c = 4 c m, β = ∠ O S Q, α = ∠ S O Q$ och $γ = 180 - ∠ S O Q - ∠ O S Q$ .

Så du har då $O Q = 4 * \frac{\sin (∠ O S Q)}{\sin (180 - ∠ S O Q - ∠ O S Q)} \approx 1.33 c m$

Baserat på uppställningen (givet att den är tolkad rätt) ovan borde OQ bli 1.33 cm.

Men det finns naturligtvis fler sätt att lösa OQ på. Du ser säkert en annan lösning än mig efter du läst några rader.

En annan lösning är att du har två trianglar OSP och OQS. Eftersom dessa är rätvinkliga båda två, den ena i Q och den andra i S (jag tror att man inte behöver bevisa att tangenten är vinkelrät mot radien) och delar vinkeln vid O är dessa likformiga och vi kan ställa upp $\frac{O Q}{O S} = \frac{O S}{O P}$

Om vi löser ut OQ får vi: $O Q = \frac{O S^{2}}{O P} = \frac{4^{2}}{12} = \frac{4}{3}$

Svara