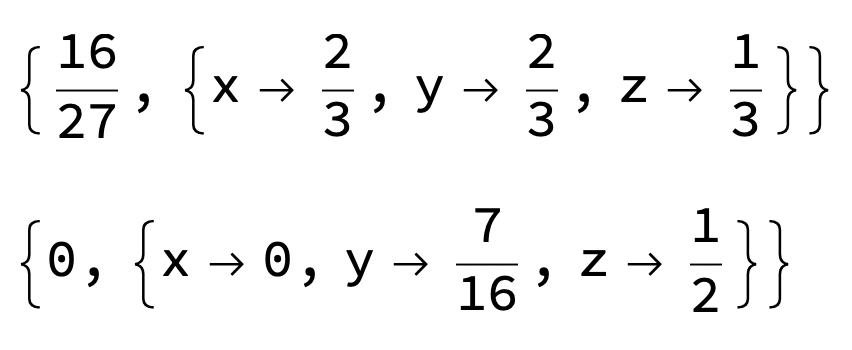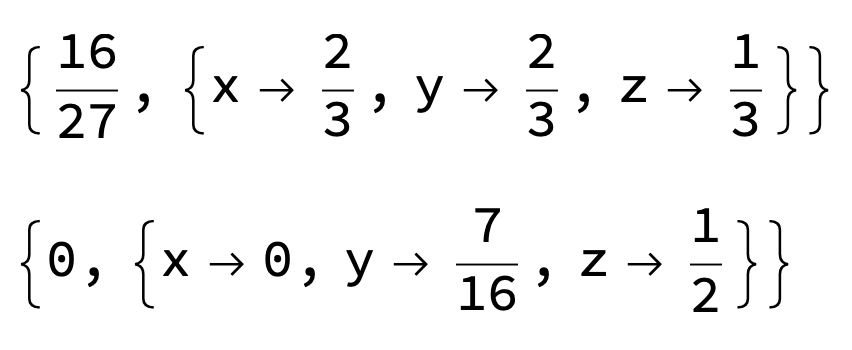Bestäm största och minsta värdet i området (Matematik/Universitet/Flervariabelanalys)

Trevlig uppgift, men jag gissar att den har en "uppenbar" lösning (som jag inte ser direkt). Det finns en länge och mera "beräkningsintensiv". Jag avvaktar lite och ser vem som kanske har en bättre lösning.

Vad händer när du löser den ”som vanligt”? (Kollar funktionens stationära punkter samt randunkter för område.)

Trinity2 skrev:
Trevlig uppgift, men jag gissar att den har en "uppenbar" lösning (som jag inte ser direkt). Det finns en länge och mera "beräkningsintensiv". Jag avvaktar lite och ser vem som kanske har en bättre lösning.

Detta är vad jag fått för stationär punkt. Fett lång lösning men men..

Jag lyckades hitta funktionsvärdet i den stationära punkten men sen vet jag inte hur man gör med randen samt hörnen.

MrPotatohead skrev:
Vad händer när du löser den ”som vanligt”? (Kollar funktionens stationära punkter samt randunkter för område.)

Randpunkterna är väl x>=0 , y>=0 ,z>=0 samt x^2+y^2+z^2<=1?

Jag ritade upp detta men får endast denna bild och jag vet inte hur man gör sen när man undersöker randpunkterna.

Har du en ide om hur området ser ut?

Lasse Vegas skrev:
Har du en ide över hur området ser ut?

Se figuren ovan. Ritade upp detta i geogebra

Men är det så du tänker att den ser ut?

Vad representerar olikheten x^2 + y^2 + z^2 <= 1 geometriskt?

Lasse Vegas skrev:
Vad representerar olikheten x^2 + y^2 + z^2 <= 1 geometriskt?

En sfär?

Ja.

Om man kombinerar det med att x,y,z alla är >=0, vad får vi då?

Ja en svär eller egentligen ett klot eftersom vi inkluderar alla punkter inuti. Så det är ett klot med radie 1 och centrum i origo. Men en del av klotet avgränsas på grund av de andra olikheterna. x >= 0, y >= 0 och z >= 0 avgränsar området till första oktanten i 3d-koordinatsystemet.

Lyckades du lösa uppgiften? När man väl kollar randen blir det nog enklast om man använder polära koordinater.

Lasse Vegas skrev:
Lyckades du lösa uppgiften? När man väl kollar randen blir det nog enklast om man använder polära koordinater.

Nej jag är fast fortfarande

Bedinsis skrev:
Ja.

Om man kombinerar det med att x,y,z alla är >=0, vad får vi då?

Hur menar du?

En åttondels sfär.

I vad som Lasse Vegas kallade "första oktanten".

Bedinsis skrev:
En åttondels sfär.

I vad som Lasse Vegas kallade "första oktanten".

Hur vet man det? Vad innebär första oktanen?

På samma sätt som ett 2d-koordinatsystem kan delas in i kvadranter kan ett 3d-koordinatsystem delas in i okatanter.

Men det går att komma fram till områdets utseende genom att prova sig fram. Vi vet att området är ett klot. Om vi låter x >= 0 får vi endast delen av klotet där x >= 0. Vi har alltså ett halvt klot då. Sedan kan man göra samma sak med y >= 0 och z >= 0.

destiny99 skrev:
Trinity2 skrev:
Trevlig uppgift, men jag gissar att den har en "uppenbar" lösning (som jag inte ser direkt). Det finns en länge och mera "beräkningsintensiv". Jag avvaktar lite och ser vem som kanske har en bättre lösning.

Detta är vad jag fått för stationär punkt. Fett lång lösning men men..

Jag lyckades hitta funktionsvärdet i den stationära punkten men sen vet jag inte hur man gör med randen samt hörnen.

Mathematica ger max och min:

Det stämmer att min är noll men det finns flera olika punkter som ger min-värdet.

Trinity2 skrev:
destiny99 skrev:
Trinity2 skrev:
Trevlig uppgift, men jag gissar att den har en "uppenbar" lösning (som jag inte ser direkt). Det finns en länge och mera "beräkningsintensiv". Jag avvaktar lite och ser vem som kanske har en bättre lösning.

Detta är vad jag fått för stationär punkt. Fett lång lösning men men..

Jag lyckades hitta funktionsvärdet i den stationära punkten men sen vet jag inte hur man gör med randen samt hörnen.

Mathematica ger max och min:

trinity jag fick också stationära punkten (2/3,2/3,1/3) och samma funktionsvärde för denna punkt. Jag fick även stationära punkten 0 samt funktionsvärdet 0. men hur fick du övriga punkterna där x=0, y=7/16 och z=1/2

Alternativ algebraisk lösning som utnyttjar QM-AM-GM-HM-olikheterna (https://en.wikipedia.org/wiki/QM-AM-GM-HM_inequalities):

Visa spoiler

Maximum:

$\displaystyle xyz+xy \stackrel{\text{AM-QM}}{\leq} \frac{x^{2}+y^{2}}{2}z + \frac{x^{2}+y^{2}}{2} = \frac{(x^{2}+y^{2})(z+1)}{2} \leq \frac{(1-z^{2})(z+1)}{2} \\= \frac{(z+1)^{2}(1-z)}{2} = \frac{(z+1) \cdot (z+1) \cdot 2(1-z)}{4} \stackrel{\text{AM-GM}}{\leq} \frac{((z+1) + (z+1) + 2(1-z))^{3}}{4 \cdot 27} \\= \frac{4^{3}}{4 \cdot 27} = \frac{16}{27}$

Likhet sker om och endast om $x=y$ , $x^{2}+y^{2}+z^{2}=1$ och $z+1=2(1-z)$ dvs. $x=y=2/3$ och $z=1/3$ .

Minimum:

$xyz+xy=xy(z+1) \geq 0$

för alla $x,y,z \geq 0$ . Likhet sker om och endast om $x=0$ eller $y=0$ då $z+1>0$ .

destiny99 skrev:
Trinity2 skrev:
destiny99 skrev:
Trinity2 skrev:
Trevlig uppgift, men jag gissar att den har en "uppenbar" lösning (som jag inte ser direkt). Det finns en länge och mera "beräkningsintensiv". Jag avvaktar lite och ser vem som kanske har en bättre lösning.

Detta är vad jag fått för stationär punkt. Fett lång lösning men men..

Jag lyckades hitta funktionsvärdet i den stationära punkten men sen vet jag inte hur man gör med randen samt hörnen.

Mathematica ger max och min:

trinity jag fick också stationära punkten (2/3,2/3,1/3) och samma funktionsvärde för denna punkt. Jag fick även stationära punkten 0 samt funktionsvärdet 0. men hur fick du övriga punkterna där x=0, y=7/16 och z=1/2

Jag bara frågade Math.... och den gav "något svar". Vet ej vad den grundar sig på. Kanske någon halvbra "AI". Eftersom koordinaterna ej efterfrågas kan man bara bortse från det givna svaret. Den verkar ha problem med generella lösningar.

Det er ut som Månsson/Norbeck så jag gissar på att boken innehåller en mängd exempel så visar på hur 'de' vill att den skall lösas.

Trinity2 skrev:
destiny99 skrev:
Trinity2 skrev:
destiny99 skrev:
Trinity2 skrev:
Trevlig uppgift, men jag gissar att den har en "uppenbar" lösning (som jag inte ser direkt). Det finns en länge och mera "beräkningsintensiv". Jag avvaktar lite och ser vem som kanske har en bättre lösning.

Detta är vad jag fått för stationär punkt. Fett lång lösning men men..

Jag lyckades hitta funktionsvärdet i den stationära punkten men sen vet jag inte hur man gör med randen samt hörnen.

Mathematica ger max och min:

trinity jag fick också stationära punkten (2/3,2/3,1/3) och samma funktionsvärde för denna punkt. Jag fick även stationära punkten 0 samt funktionsvärdet 0. men hur fick du övriga punkterna där x=0, y=7/16 och z=1/2

Jag bara frågade Math.... och den gav "något svar". Vet ej vad den grundar sig på. Kanske någon halvbra "AI". Eftersom koordinaterna ej efterfrågas kan man bara bortse från det givna svaret. Den verkar ha problem med generella lösningar.

Det er ut som Månsson/Norbeck så jag gissar på att boken innehåller en mängd exempel så visar på hur 'de' vill att den skall lösas.

Jo det är månsson boken men just denna uppgift saknar lösningsförslag.

destiny99 skrev:
Trinity2 skrev:
destiny99 skrev:
Trinity2 skrev:
destiny99 skrev:
Trinity2 skrev:
Trevlig uppgift, men jag gissar att den har en "uppenbar" lösning (som jag inte ser direkt). Det finns en länge och mera "beräkningsintensiv". Jag avvaktar lite och ser vem som kanske har en bättre lösning.

Detta är vad jag fått för stationär punkt. Fett lång lösning men men..

Jag lyckades hitta funktionsvärdet i den stationära punkten men sen vet jag inte hur man gör med randen samt hörnen.

Mathematica ger max och min:

trinity jag fick också stationära punkten (2/3,2/3,1/3) och samma funktionsvärde för denna punkt. Jag fick även stationära punkten 0 samt funktionsvärdet 0. men hur fick du övriga punkterna där x=0, y=7/16 och z=1/2

Jag bara frågade Math.... och den gav "något svar". Vet ej vad den grundar sig på. Kanske någon halvbra "AI". Eftersom koordinaterna ej efterfrågas kan man bara bortse från det givna svaret. Den verkar ha problem med generella lösningar.

Det er ut som Månsson/Norbeck så jag gissar på att boken innehåller en mängd exempel så visar på hur 'de' vill att den skall lösas.

Jo det är månsson boken men just denna uppgift saknar lösningsförslag.

Är där ingen före med "L" i kanten?

Trinity2 skrev:
destiny99 skrev:
Trinity2 skrev:
destiny99 skrev:
Trinity2 skrev:
destiny99 skrev:
Trinity2 skrev:
Trevlig uppgift, men jag gissar att den har en "uppenbar" lösning (som jag inte ser direkt). Det finns en länge och mera "beräkningsintensiv". Jag avvaktar lite och ser vem som kanske har en bättre lösning.

Detta är vad jag fått för stationär punkt. Fett lång lösning men men..

Jag lyckades hitta funktionsvärdet i den stationära punkten men sen vet jag inte hur man gör med randen samt hörnen.

Mathematica ger max och min:

trinity jag fick också stationära punkten (2/3,2/3,1/3) och samma funktionsvärde för denna punkt. Jag fick även stationära punkten 0 samt funktionsvärdet 0. men hur fick du övriga punkterna där x=0, y=7/16 och z=1/2

Jag bara frågade Math.... och den gav "något svar". Vet ej vad den grundar sig på. Kanske någon halvbra "AI". Eftersom koordinaterna ej efterfrågas kan man bara bortse från det givna svaret. Den verkar ha problem med generella lösningar.

Det er ut som Månsson/Norbeck så jag gissar på att boken innehåller en mängd exempel så visar på hur 'de' vill att den skall lösas.

Jo det är månsson boken men just denna uppgift saknar lösningsförslag.

Är där ingen före med "L" i kanten?

Det gäller fråga 4.14 uppgiften och inte 4.15

destiny99 skrev:
Trinity2 skrev:
destiny99 skrev:
Trinity2 skrev:
destiny99 skrev:
Trinity2 skrev:
destiny99 skrev:
Trinity2 skrev:
Trevlig uppgift, men jag gissar att den har en "uppenbar" lösning (som jag inte ser direkt). Det finns en länge och mera "beräkningsintensiv". Jag avvaktar lite och ser vem som kanske har en bättre lösning.

Detta är vad jag fått för stationär punkt. Fett lång lösning men men..

Jag lyckades hitta funktionsvärdet i den stationära punkten men sen vet jag inte hur man gör med randen samt hörnen.

Mathematica ger max och min:

trinity jag fick också stationära punkten (2/3,2/3,1/3) och samma funktionsvärde för denna punkt. Jag fick även stationära punkten 0 samt funktionsvärdet 0. men hur fick du övriga punkterna där x=0, y=7/16 och z=1/2

Jag bara frågade Math.... och den gav "något svar". Vet ej vad den grundar sig på. Kanske någon halvbra "AI". Eftersom koordinaterna ej efterfrågas kan man bara bortse från det givna svaret. Den verkar ha problem med generella lösningar.

Det er ut som Månsson/Norbeck så jag gissar på att boken innehåller en mängd exempel så visar på hur 'de' vill att den skall lösas.

Jo det är månsson boken men just denna uppgift saknar lösningsförslag.

Är där ingen före med "L" i kanten?

Det gäller fråga 4.14 uppgiften och inte 4.15

Och den är ej snarlik?

Om man skriver om f som du gjort

och går över till polära koordinater;

där 0≤r≤1 och 0≤t≤π/2

ser vi att sin(2t) är max (=1) för 2t=π/2 vilket ger t=π/4.

I π/4 riktning är allså funkionen maximal avs sin-faktorn.

Vi kan då skriva

g(t)=r^2/2(1+sqrt(1-r^2)

som ser ut enl.

g'(t)ges av

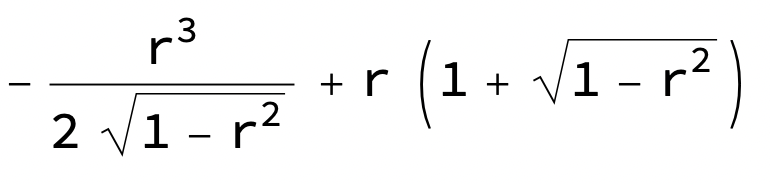
och ekv. g'(t)=0 gör att r kan divideras 'bort' (r=/=0) och kvar blir en ekvation som efter kvadrering förenklas till r^2=8/9 vilket ger r_0=2sqrt(2)/3 då r≥0

Tecken studie ger att det är max (eller 2:a derivata).

Max är därmed

g(r_0)=16/27

Ytan ser ut så här

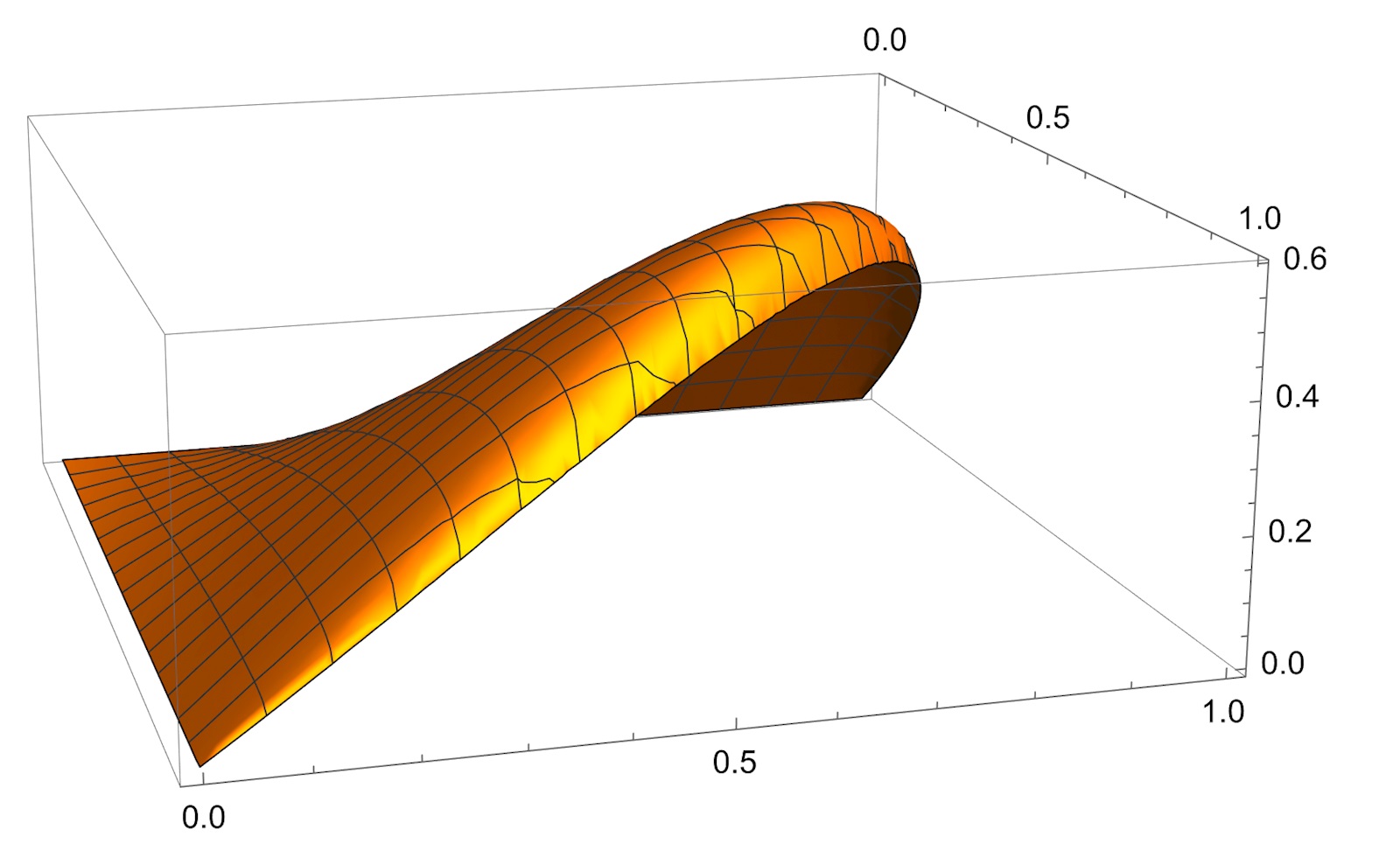
g(t)≥0 för t i området varför g_min=0 vilket ges antages på r- och t-axlarna