Bestäm största och minsta värde
Hej! Jag har lite problem med den här uppgiften. Först är jag osäker på hur de kan konstatera att inte är i definitonsmängden. Det enda sättet jag kan komma på att kolla det är med enhetscirkeln då värdena ger 45 grader på den och cirkelbågen kommer ligga utanför sidan på triangeln med start och slut i (0,1) och (1,0).
Sen blir jag också förvirrad när de kollar randen. På x=0 och y=0 konstateras det bara att det inte är några stationära punkter. Men jag trodde att det inte behöver vara en stationär punkt på rannden för att vara en max/minpunkt och att det är därför man kollar den?
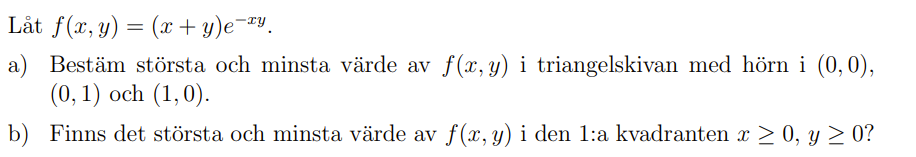

(1/sqrt(2),1/sqrt(2)) ligger på randen. Eftersom att de ändå ska kolla randen efter bortser de från denna punkt i detta läge. Här fokuserar de på inre punkter.
När de sedan kollar de ränderna utforskar de stationära punkter. Eftersom att det inte finns sådana räcker det med att kolla hörnpunkterna, vilket är "randen av randen". Detta är alltså precis samma som i första steget, men för en lägre dimension.
Tack för förklaringen!
Ligger punkten på randen? Alltså triangelns hypotenusa? Jag tänkte att den låg på enhetscirkeln, vilken ligger utanför D, men jag är kanske fel på det.
Så här tänkte jag (det ska vara enhetscirkeln):
Är de att de kollar f'x=0 och f'y=0 men ej skriver ut det? Annars förstår jag ej hur de direkt kan säga att det inte finns några stationära punkter efter vad de har räknat
Du har rätt, punkten ligger utanför triangeln.


