Bestäm största möjliga area på triangel

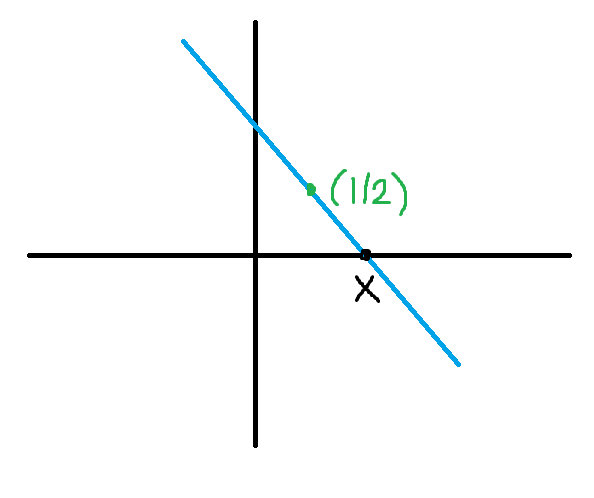
En linje inneslutar tillsammans med de positiva koordinataxlarna ett triangulärt område. Linjen går genom punkten $(1 | 2)$ . Bestäm triangelns största möjliga area.

Hittils har jag kommit fram till att uttrycket för triangelns area är:

$A (x) = \frac{x f (x)}{2} = \frac{k x^{2} + m x}{2} = \frac{1}{2} k x^{2} + \frac{1}{2} m x$

Dessutom har vi sambandet $f (1) = 2 = k + m$

$\Rightarrow m = 2 - k \Rightarrow A (x) = \frac{1}{2} k x^{2} + \frac{1}{2} (2 - k) x$

Då detta är en andragradsfunktion borde man kunna ta fram symmetrilinjen:
$\frac{- b}{2 a} = \frac{\frac{k - 2}{2}}{k} = \frac{k - 2}{2 k}$

Sedan ville jag stoppa in detta i min funktion $A (x)$ för att se vilket det största värdet skulle vara (uttryckt i k), men av någon anledning blir

$A (\frac{k - 2}{2 k}) = 0$

Jag fattar verkligen inte varför eller vad jag ska göra. Hjälp uppskattas.

Börja med att rita, så ser du nog hur du ska formulera problemet.

Jag hade redan ritat upp det och då ritade jag det så här:

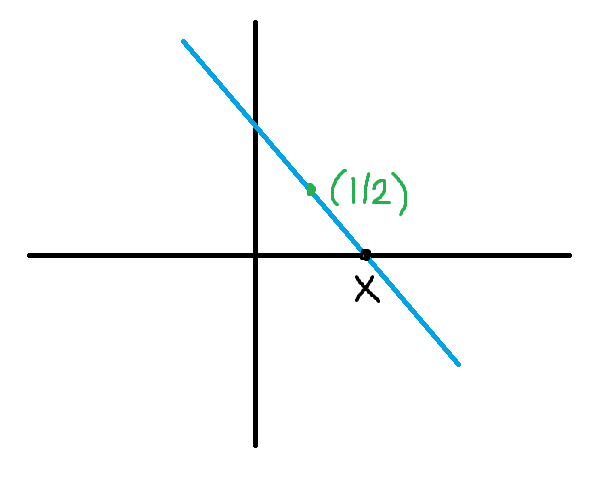
Triangelns bas blir då $x$ och dess höjd $f (x)$ . Har jag missförstått något?

Om y = f(x) är linjen så är ju y 0 där du har markerat x.

naytte skrev:
Jag hade redan ritat upp det och då ritade jag det så här:

Triangelns bas blir då $x$ och dess höjd $f (x)$ . Har jag missförstått något?

Ja, det verkar som om du har missförstått något. Om x är x-koordinaten för skärningen med x-axeln, så är f(x) = 0. Höjden är skärningspunkten med y-axeln, eller hur? Vilket x-värde har vu där?

Oj, vilken miss av mig! Jag vet inte hur jag kunde göra ett sådant fundamentalt fel. Ursäkta för min dumma fråga!

Svara

Visa senaste svar