Bestäm sannolikheten att två försök ger exakt 2 poäng och två försök ger exakt 3 poäng
Hej! Jag försökte lösa denna uppgift men får fel svar, jag tänker att man borde kunna använda sig av denna sats:



Facit:
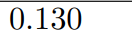
Min lösning:

Tack på förhand!
Är verkligen händelserna oberoende?
Calle_K skrev:Är verkligen händelserna oberoende?
Jag tänker att de borde vara det eftersom xi1,xi2,.... är oboeroende?
Binomialfördelningen känner du till, men den passar inte här.
Är du bekant med multinomialfördelningen?
Jag tolkar uppgiften som att Olle ska skjuta 5 pilar mot måltavlan. Av dessa ska två ge 2 poäng och två ska ge 3 poäng.
En tillåten kombination är alltså: 0, 2, 3, 2, 3
En annan tillåten kombination är: 2, 2, 3, 3, 1
1. På hur många sätt kan man placera ut 2 st 2:or och 2st 3:or på 5 försök?
2. Vad är sannolikheten för (varje sådan) tillåten kombination?
3. Vad blir den totala sannolikheten?
D4NIEL skrev:Jag tolkar uppgiften som att Olle ska skjuta 5 pilar mot måltavlan. Av dessa ska två ge 2 poäng och två ska ge 3 poäng.
En tillåten kombination är alltså: 0, 2, 3, 2, 3
En annan tillåten kombination är: 2, 2, 3, 3, 1
1. På hur många sätt kan man placera ut 2 st 2:or och 2st 3:or på 5 försök?
2. Vad är sannolikheten för (varje sådan) tillåten kombination?
3. Vad blir den totala sannolikheten?
1. Jag tänker att antal sätt att placera ut 2st 2.or på 5 försök är = antal möjliga fall
Antal sätt att placera ut 2st 3:or på 5 försök är också = antal möjliga fall
2. Sannolikheten att placera 2 2:or på 5 försök är antal gynsamma fall/ antalet möjliga fall =
Sannlokikheten att placera 2 3:or på 5 försök är också
3. totala sannolikheten blir P(placera 2:2or på 5 försök)*p(placera 2 3:or på 5 försök) =
Då jag får en sannolikhet större än 1 vet jagatt jag gjort fel men vet inte vart det blir fel?:(
Händelserna är inte oberoende. Givet att du har två 2or är sannolikheten mindre att du får två 3or (färre gynnsamma utfall kvar).
Det stämmer att Olle kan placera ut sina 2:or på sätt. Men när han placerat ut sina 2:or finns det bara 3 lediga platser kvar. Han kan alltså placera ut sina 3:or på sätt.
Totalt kan Olle placera ut sina 2:or och 3:or på
sätt. Den sista platsen upptas antingen av en 0:a eller en 1:a. Tekniskt sett kan Olle placera ut sina pilar på 60 olika sätt, 30 med en viss sannolikhet och 30 med en annan sannolikhet beroende på om sista pilen är en 0:a eller en 1:a (det går också att samla ihop dessa fall genom att slå samman sannolikheterna för 0 och 1).
Vad är sannolikheten att Olle ska skjuta 2 2:or, 2 3:or och en 0:a? (Du har 30 sådana fall). Använd tabellen du fått i uppgiften för sannolikheterna samt multiplikationsprincipen!
Vad är sannolikheten att Olle ska skjuta 2 2:or, 2 3:or och en 1:a? (Du har 30 sådana fall)
Vad blir den totala sannolikheten?
Visa spoiler
Eftersom sannolikheten för antingen ELLER är kan vi samla ihop alla fall till
Hejhej! skrev:Calle_K skrev:Är verkligen händelserna oberoende?
Jag tänker att de borde vara det eftersom xi1,xi2,.... är oboeroende?
Utfallen för var och en av pilarna är oberoende.
Kolla multinomialfördelningen för ett enklare sätt att direkt
ställa upp sannolikheten för händelser av samma typ som i uppgiften
Introduction to the Multinomial Distribution
https://youtu.be/syVW7DgvUaY?feature=shared
Visa spoiler
[(5!)/(2! · 2! · 1!)] * 0,32 · 0,42 · 0,3 = 0,1296
D4NIEL skrev:Det stämmer att Olle kan placera ut sina 2:or på sätt. Men när han placerat ut sina 2:or finns det bara 3 lediga platser kvar. Han kan alltså placera ut sina 3:or på sätt.
Totalt kan Olle placera ut sina 2:or och 3:or på
sätt. Den sista platsen upptas antingen av en 0:a eller en 1:a. Tekniskt sett kan Olle placera ut sina pilar på 60 olika sätt, 30 med en viss sannolikhet och 30 med en annan sannolikhet beroende på om sista pilen är en 0:a eller en 1:a (det går också att samla ihop dessa fall genom att slå samman sannolikheterna för 0 och 1).
Vad är sannolikheten att Olle ska skjuta 2 2:or, 2 3:or och en 0:a? (Du har 30 sådana fall). Använd tabellen du fått i uppgiften för sannolikheterna samt multiplikationsprincipen!
Vad är sannolikheten att Olle ska skjuta 2 2:or, 2 3:or och en 1:a? (Du har 30 sådana fall)
Vad blir den totala sannolikheten?
Visa spoiler
Eftersom sannolikheten för antingen ELLER är kan vi samla ihop alla fall till
Det är sant tack! Nu tror jag att jag hänger med på alla steg:) det bara finns 3 platser kvar om han placerat ut 2 2:or redan och att vi får 30 fall för 2:2or,2 3:or och en 1:a samt 30 fall att få 2 2:or, 2 3:or och en 0:a. Jag är även med på att sannolikheten för 0 eller 1 är 0,1+0,2 = 0,3. Och att vi därför får
P(xi = 5) = p(två 2:o2)*p(två 3:or)*p(en 1:a eller 1n 0:a)*antalet sätt att placera dessa 5 på=
=p(xi=2)^2*p(xi=3)^2*p(xi=0 eller 1)*antalet sätt att placera de på= = 0,1296
Tack för all hjälp och svar!:)


