Bestäm sannolikheten att han måste skriva tentan minst 2 men högst 5 gånger
Hej! Jag försöker förstå hur de gjort i facit. MIn första tanke när jag såg den här uppgiften var att om xi = antalet gånger han måste skriva tentan så tillhör xi Bin (n;0,8) men jag fick problem att fortsätta på det spåret då jag inte viste vad n var eftersom en ska vara mellan 2 och 5. Jag antar dock att det är liknande sätt de tänkt i facit och att det är så de löst uppgiften. Det jag inte förstår dock är varför man just tar 0,8^x-1 och 0,2 upphöjt till ingenting? Då sannolikhetsformeln för en binomialfördelning är:
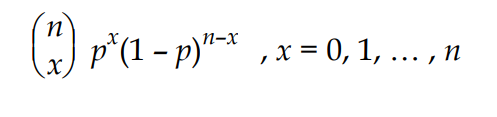

Facit: 0,472
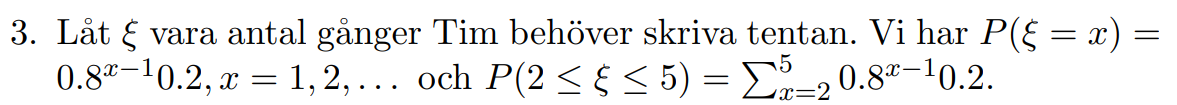
Tack på förhand!
P(2) är chansen att klara tentan på precis andra försöket.
Det är 20% chans att lyckas och då måste han förstås ha misslyckas på första, vilket är 80% "chans" att göra.
P(3) är chansen att misslyckas två gånger och sedan lyckas på tredje:
Det ger:
sictransit skrev:P(2) är chansen att klara tentan på precis andra försöket.
Det är 20% chans att lyckas och då måste han förstås ha misslyckas på första, vilket är 80% "chans" att göra.
P(3) är chansen att misslyckas två gånger och sedan lyckas på tredje:
Det ger:
Tack! jag förstår inte dock, vad händer med exponenten till 0,2? (n-x)
Det här är jag inte särskilt bra på. Min uppställning var bara hur jag spontant löste problemet. Har jag läst detta på universitetet så var det 30+ år sedan och glömt/preskriberat sedan länge. :-)
Är du säker på att binomialfördelning går att tillämpa här? Vad jag minns är det antal framgångar givet ett antal försök. Typ att han skriver tentan 10 gånger och vi vill veta hur många gånger han borde klara sig.
Här är det en geometrisk fördelning, eller egentligen summan av flera (2-5), alltså sannolikheten att han klarar sig 2:a, 3:e, ... 5:e gången efter att ha misslyckats tidigare.
Det som INTE uppfyller "minst 2 men högst 5 gånger" är
- Han klarar första tentan.
- Han missar alla fem tentorna.
sictransit skrev:Det här är jag inte särskilt bra på. Min uppställning var bara hur jag spontant löste problemet. Har jag läst detta på universitetet så var det 30+ år sedan och glömt/preskriberat sedan länge. :-)
Är du säker på att binomialfördelning går att tillämpa här? Vad jag minns är det antal framgångar givet ett antal försök. Typ att han skriver tentan 10 gånger och vi vill veta hur många gånger han borde klara sig.
Här är det en geometrisk fördelning, eller egentligen summan av flera (2-5), alltså sannolikheten att han klarar sig 2:a, 3:e, ... 5:e gången efter att ha misslyckats tidigare.
Jag vet inte men jag tycker det såg ut som formeln för en binomialfördelning:) , får dock inte riktigt ihop det:( hittar inget i boken om geometriska fördelningar förutom den hypergeometriska men jag tycker inte dess formel stämmer överrens med den här uppställningen?
Men du köper hur jag (och facit) resonerar? Chansen är 0,2 att klara tentan varje gång och sannolikheten att inte klara den innan försök n är 0,8n-1.
sictransit skrev:Men du köper hur jag (och facit) resonerar? Chansen är 0,2 att klara tentan varje gång och sannolikheten att inte klara den innan försök n är 0,8n-1.
Ahh jo nu förstår jag:) hoppas jag förstått rätt:D Det är nog en binomialfördelning för då får vi om man jämför med formeln så är ju n antalet gånger händelsen sker. I vårat fall är det antalet gånger han måste skriva tentan vilket är en mer än antalet gånger han failar tentan. Antalet gånger han måste skriva tentan = x så antalet gånger han failar tentan är x-1, därav x-1 som exponent för sannolikheten 0,8 (att faila tentan). Det gör också att antalet gånger han måste skriva tentan n = x + 1 vilket ger att exponenten till sannolikheten att klara tentan 0,2 blir n-x = x+1-x=1 vilket ger 0,2^1. Den enda termen jag fastnar på nu dock är (n över x) i binomialfördelningen:(
Hejhej! skrev:Den enda termen jag fastnar på nu dock är (n över x) i binomialfördelningen:(
Om han klarar tentan på fyra försök, så är det inte samma sak som att han klarar en av fyra tentor.
Det är däremot samma sak som att han missar första, andra och tredje tentan, och därefter klarar fjärde tentan.
För övrigt tycker jag att den metod jag antydde blir mycket enklare.
Bubo skrev:Hejhej! skrev:Den enda termen jag fastnar på nu dock är (n över x) i binomialfördelningen:(
Om han klarar tentan på fyra försök, så är det inte samma sak som att han klarar en av fyra tentor.
Det är däremot samma sak som att han missar första, andra och tredje tentan, och därefter klarar fjärde tentan.
För övrigt tycker jag att den metod jag antydde blir mycket enklare.
Det är sant, det kanske inte är en binomialfördelning trots allt? får inte till första delen av ekvationen:(
Ah nu tror jag att jag förstår metoden du skrev ovan! Jo det känns enklare tack!:)
P(han måste skriva tentan minst 2 men högst 5 gånger) = 1 - P(Han måste skriva tentan en gång eller han måste skriva tentan mer än 5 gånger) = 1 - p(han klarar första tentan eller han failar alla 5 tentor) = 1 -(P(han klarar första tentan) + P(Han failar 5 tentor)) = 1 -(0,2 + 0,8^5) = 1-0,52768 = 0,472
En binomialfördelning är det inte. I så fall skulle han skriva tentan ett bestämt antal gånger och så skulle man räkna hur många gånger han klarar den, och det är inte fallet här.
Säg att sannolikheten att klara tentan är p och att kuggas är q. Det ger
Sh klarar på 2 försök: qp
Sh klarar på 3 försök: qqp
…. på 4 försök: qqqp
…. på 5 försök: qqqqp
Vi vet p och q så det är bara att addera.
Marilyn skrev:En binomialfördelning är det inte. I så fall skulle han skriva tentan ett bestämt antal gånger och så skulle man räkna hur många gånger han klarar den, och det är inte fallet här.
Säg att sannolikheten att klara tentan är p och att kuggas är q. Det ger
Sh klarar på 2 försök: qp
Sh klarar på 3 försök: qqp
…. på 4 försök: qqqp
…. på 5 försök: qqqqp
Vi vet p och q så det är bara att addera.
Ah okej tack! Det var också en smart lösning!

