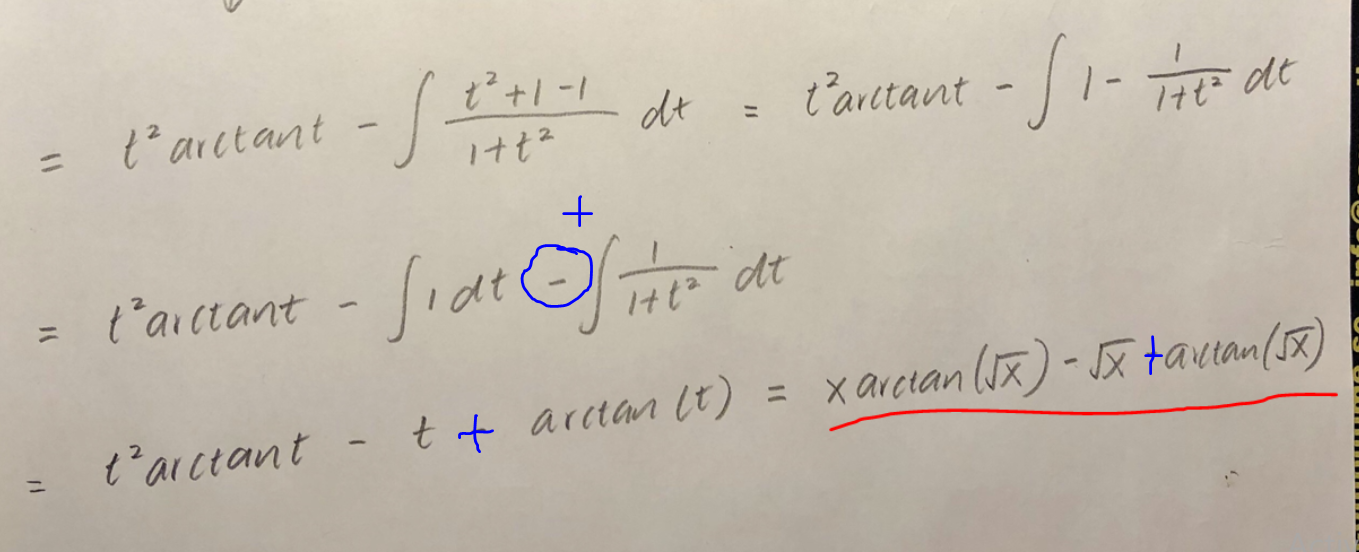Bestäm samtliga primitiva funktioner till arctan(sqrt(x))

Du kan ju alltid kontrollderivera. 

Finns det enklare sätt. Jag vill verkligen inte deriverar en sånt komplicerat uttryck. 

Bästa sättet att veta om man har integrerat rätt är att derivera resultatet. 

Derivera är i regel enklare än att integrera. Kontrollderivering räddar många poäng på tentorna när man har slarvat. 

"Enklare" är väl att kolla med Wolfram alpha, men det är inte riktigt samma sak som att räkna själv. 

Så här har jag deriverat. 

Vad jag ser så deriverar du rätt, och förenklar rätt fram till det inringade. Derivatan blir inte vad den borde, så du har integrerat fel. 

Om du ändrar tecken på din sista term så bli der rätt, se blå plustecken. 

Du har gjort rätt men du har slarvat. 

Kan du hitta vart du gjort fel? 

Det börjar i rad 3, när du bryter isär bråket.

Notera att jag syftar på din integrering, inte derivering eftersom Dr. G redan gett dig feedback om den delen.

Dr. G skrev:

Vad jag ser så deriverar du rätt, och förenklar rätt fram till det inringade. Derivatan blir inte vad den borde, så du har integrerat fel. 

Om du ändrar tecken på din sista term så bli der rätt, se blå plustecken. 

$$\begin{gathered} Så \frac{d}{dx}(xarc\tan \sqrt{x}-\sqrt{x}-arc\tan \sqrt{x})=arc\tan \sqrt{x}-\frac{\sqrt{x}}{(x+1)} \\ den här delen har ja gjort rätt. \end{gathered}$$

Dracaena skrev:

Du har gjort rätt men du har slarvat. 

Kan du hitta vart du gjort fel? 

Det börjar i rad 3, när du bryter isär bråket.

Notera att jag syftar på din integrering, inte derivering eftersom Dr. G redan gett dig feedback om den delen.

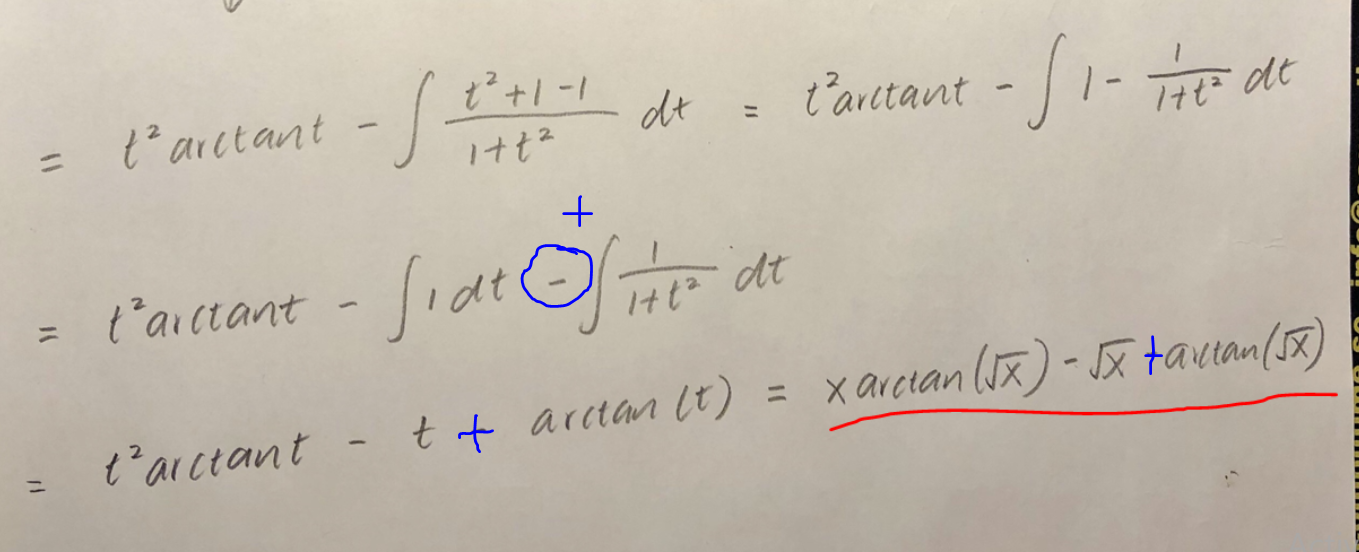
Där (blå markerat) borde bli en + tecken istället. eller hur? 

Så när ja deriverar uttrycket: $x arc\tan \left(\sqrt{x}\right)-\sqrt{x}+arc\tan \left(\sqrt{x}\right)$så borde ja får $arc\tan \left(\sqrt{x}\right)$. 

Marcus N skrev:

Dracaena skrev:

Du har gjort rätt men du har slarvat. 

Kan du hitta vart du gjort fel? 

Det börjar i rad 3, när du bryter isär bråket.

Notera att jag syftar på din integrering, inte derivering eftersom Dr. G redan gett dig feedback om den delen.

Där (blå markerat) borde bli en + tecken istället. eller hur? 

Ja, precis, minustecknet innesluter båda integralerna när du splittrar den. Ett tips är att använda paranteser även om du känner att du har koll på tecken. Det är så enkelt att man glömmer bort sig efter man kört pbu, rättat ett slarvfel någonstans, gjort en sub etc.