Bestäm polynomet p(x)
I facit gjordes denna beräkning:
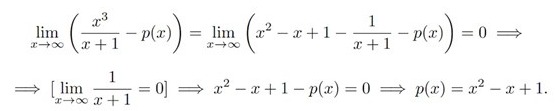
Är det ok att i andra ledet bara plocka bort gränsvärdet? Det gjordes en gränsvärdes beräkning av kvoten men resten lämnades ute för att sedan göras till en ekvation. Har fått lära mig att alla variablerna i gränsvärdena måste beräknas samtidigt, någonting som inte verkar göras här.
Mellan steg 1 och steg 2 görs bara en omformning av uttrycket genom att utföra divisionen och ingen gränsvärdesberäkning, så det är faktiskt olämpligt att skriva ”lim” där. Tredje steget beror inte på något av de föregående, så där bör implikationssymbolen tas bort. Jag skulle hellre skriva ”Vi har….” följt av (den triviala) gränsvärdesbestämningen. Därefter ett ”Således” följt av den återstående texten med ett ”lim” framför uttrycket.
Tomten skrev:Mellan steg 1 och steg 2 görs bara en omformning av uttrycket genom att utföra divisionen och ingen gränsvärdesberäkning, så det är faktiskt olämpligt att skriva ”lim” där. Tredje steget beror inte på något av de föregående, så där bör implikationssymbolen tas bort. Jag skulle hellre skriva ”Vi har….” följt av (den triviala) gränsvärdesbestämningen. Därefter ett ”Således” följt av den återstående texten med ett ”lim” framför uttrycket.
Jag håller med dig, förutom att lim ändå borde stå kvar efter första likhetstecknet. Annars gäller ju inte likheten.
Ok, tack!
Men jag förstår fortfarande inte riktigt varför hela gränsvärdesberäkningen försvinner bara för att ?
Man kan ha kvar mellansteget där x går mot oändligheten för x2-x+1-p(x), och här har de hoppat över det och direkt dragit slutsatsen att x2-x+1-p(x) måste vara 0 för att det gränsvärdet ska existera.
Laguna skrev:Man kan ha kvar mellansteget där x går mot oändligheten för x2-x+1-p(x), och här har de hoppat över det och direkt dragit slutsatsen att x2-x+1-p(x) måste vara 0 för att det gränsvärdet ska existera.
Jag förstår inte riktigt hur man kommer fram till den slutsatsen.... Gränsvärdet blir väl bara oändligt?
Nej, vi kan välja p(x) så att x2-x+1-p(x) = 0, och då är gränsvärdet 0.



