Bestäm polynomet
Hej
Jag ska lösa denna:

Och jag har gjort såhär
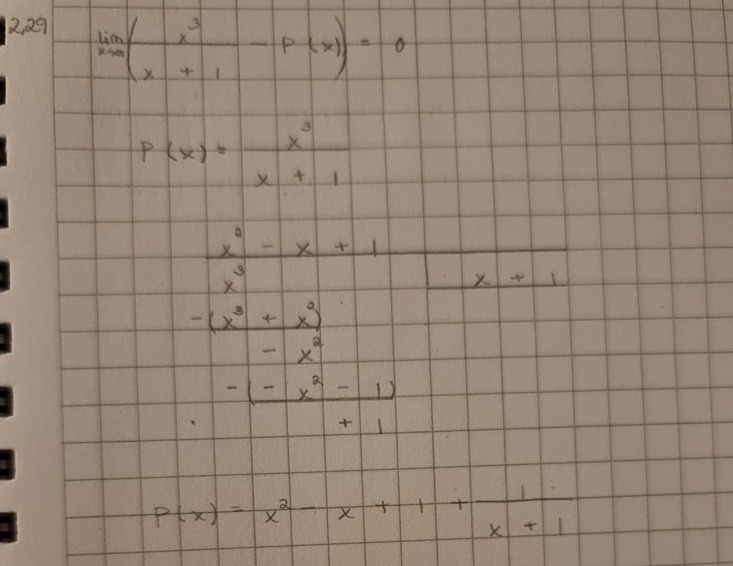
Men svaret är bara x^2-x+1; varför är det så?
Du vill att x3/(x+1) - p(x) skall gå mot noll, där p(x) är ett polynom.
Du har visat att x3/(x+1) = x2 - x + 1 + 1/(1+x).
Så vilket polynom p(x) krävs för att x2 - x + 1 + 1/(1+x) - p(x) skall gå mot noll?
PATENTERAMERA skrev:Du vill att x3/(x+1) - p(x) skall gå mot noll, där p(x) är ett polynom.
Du har visat att x3/(x+1) = x2 - x + 1 + 1/(1+x).
Så vilket polynom p(x) krävs för att x2 - x + 1 + 1/(1+x) - p(x) skall gå mot noll?
Vänta, menar du att jag ska sätta in p i funktionen eller förstår inte hur jag ska tänka annars? Varför är det den funktionen jag fick fram minus p? Jag trodde att det var p
Du skall hitta ett polynom p(x) sådant att x3/(x+1) - p(x) går mot noll.
Du hade med polynomdivision visat att x3/(x+1) = x2 - x + 1 + 1/(1+x) (jag tror det skall vara -1/(1+x) på slutet).
Således behöver vi hitta ett polynom p(x) sådant att
x2 -x + 1 - 1/(1+x) - p(x) går mot noll. Kan du tänka ut vilket polynom det blir?
PATENTERAMERA skrev:Du skall hitta ett polynom p(x) sådant att x3/(x+1) - p(x) går mot noll.
Du hade med polynomdivision visat att x3/(x+1) = x2 - x + 1 + 1/(1+x) (jag tror det skall vara -1/(1+x) på slutet).
Således behöver vi hitta ett polynom p(x) sådant att
x2 -x + 1 - 1/(1+x) - p(x) går mot noll. Kan du tänka ut vilket polynom det blir?
- det jag fick ut?
Vad fick du ut?
PATENTERAMERA skrev:
Vad fick du ut?
Menar det jag fick ut från polynomdivisionen fast ett minus innan så jag byter tecken på allting?
Ett alternativt tillvägagångssätt är att ansätta
p(x)=ax2+bx+c
och identifiera koefficienterna. Tänk på att en konstant delad med (x+1) går mot noll.
Heocon skrev:PATENTERAMERA skrev:
Vad fick du ut?
Menar det jag fick ut från polynomdivisionen fast ett minus innan så jag byter tecken på allting?
Du gör ett litet tankefel. Det gäller att hitta ett polynom p(x) så att x3/(1+x) - p(x) går mot noll då x går mot oändlighet.
Du tror då att det innebär att p(x) = x3/(x+1). Det är naturligtvis inte korrekt då två uttryck inte behöver vara exakt samma bara för att de blir mer och mer lika för stora värden på x. Dessutom är HL inte ett polynom så redan där borde du misstänka att något gått fel.
Läs igenom tråden igen och se om du inte kan komma fram till lösningen. Annars kan du testa förslaget i #8.
PATENTERAMERA skrev:Heocon skrev:PATENTERAMERA skrev:
Vad fick du ut?
Menar det jag fick ut från polynomdivisionen fast ett minus innan så jag byter tecken på allting?
Du gör ett litet tankefel. Det gäller att hitta ett polynom p(x) så att x3/(1+x) - p(x) går mot noll då x går mot oändlighet.
Du tror då att det innebär att p(x) = x3/(x+1). Det är naturligtvis inte korrekt då två uttryck inte behöver vara exakt samma bara för att de blir mer och mer lika för stora värden på x. Dessutom är HL inte ett polynom så redan där borde du misstänka att något gått fel.
Läs igenom tråden igen och se om du inte kan komma fram till lösningen. Annars kan du testa förslaget i #8.
Jag tror jag fattar vad ni menar: att jag ska tänka att någon funktion ska göra så hela gränsvärdet går mot 0. Men när jag tittar på den angivna I uppgiften eller den jag fick fram så "ser" jag inget://
Finns det något sätt man kan räkna ut detta eller måste jag tänka mig fram? För har tittat på de här funktionerna ett tag nu men kommer inte på vad p(x) ska vara

Termen 1/(x+1) kommer att gå mot 0 när x går mot oändligheten. Resten av uttrycket skall vara lika med 0 för alla värden på x.
Smaragdalena skrev:Termen 1/(x+1) kommer att gå mot 0 när x går mot oändligheten. Resten av uttrycket skall vara lika med 0 för alla värden på x.
Aha jag fattar nu. Den är inte med så därför är det bara x^2-x+1 för p(x), tack🥹🥹



