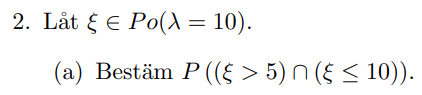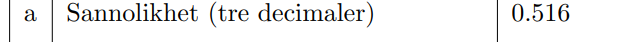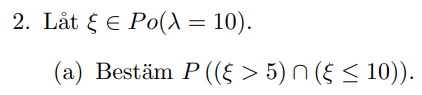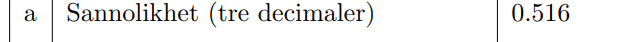Bestäm P((xi>5) snitt (xi<=10))
Hej! Jag försökte lösa denna uppgift men fick fel svar. Jag har försökt både räkna på det och använta tabellvärdena men tabellvärdet visar samma som min uträkning i princip (min uträkning gav 0,0608... och tabellvärdet gav 0,0671) så det måste vara innan denna uträkning jag gör fel. Men borde man inte kunna subtrahera 5 från 10 och beräkna p(xi<=5) som jag gjort?
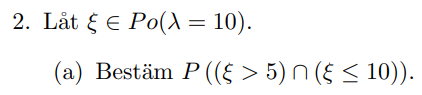
Facit:
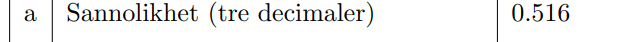
Min lösning:

Tack på förhand!
Jag kom precis på att när det är snitt kanske jag kan göra så här istället:

Jag kom närmare rätt svar som är 0,516 men det är fortfarande inte riktigt rätt svar:(
Händelserna är inte oberoende, så produkten av deras sannolikheter
är inte lika med sannolikheten för deras snitt
Arktos skrev:Händelserna är inte oberoende, så produkten av deras sannolikheter
är inte lika med sannolikheten för deras snitt
Men innebär inte oberoende att händelserna kan ske samtidigt? och xi kan vara både större än 5 och mindre än 10?
Nej, då är de disjunkta, dvs höggradigt beroende.
Hejhej! skrev:Hej! Jag försökte lösa denna uppgift men fick fel svar. Jag har försökt både räkna på det och använta tabellvärdena men tabellvärdet visar samma som min uträkning i princip (min uträkning gav 0,0608... och tabellvärdet gav 0,0671) så det måste vara innan denna uträkning jag gör fel. Men borde man inte kunna subtrahera 5 från 10 och beräkna p(xi<=5) som jag gjort?
Facit:
Min lösning:
Tack på förhand!
Du ser ut att enbart ha beräknat. P(ksi ≤ 5)
Ditt andra likhetstecken stämmer inte
Arktos skrev:Nej, då är de disjunkta, dvs höggradigt beroende.
Men disjunkta händelser kan väl inte ske samtidigt?
Nej, det är just det de inte kan
Arktos skrev:Hejhej! skrev:Hej! Jag försökte lösa denna uppgift men fick fel svar. Jag har försökt både räkna på det och använta tabellvärdena men tabellvärdet visar samma som min uträkning i princip (min uträkning gav 0,0608... och tabellvärdet gav 0,0671) så det måste vara innan denna uträkning jag gör fel. Men borde man inte kunna subtrahera 5 från 10 och beräkna p(xi<=5) som jag gjort?
Facit:
Min lösning:
Tack på förhand!
Du ser ut att enbart ha beräknat. P(ksi ≤ 5)
Ditt andra likhetstecken stämmer inte
Menar du när jag räknar ihop alla sannolikheterna?
Ja
Arktos skrev:Ja
Hm vad konstogt jag får samma svar igen när jag dubbelräknar:( och det stämmer ju med tabellvärdet?
Felet ligger i början av ditt resonemang,
där du hastigt i en radbrytning skriver att P(5 < X ≤ 10) = P(X ≤ 5)
vilket förstås är fel.
Arktos skrev:Händelserna är inte oberoende, så produkten av deras sannolikheter
är inte lika med sannolikheten för deras snitt
Men varför är de beroende? jag tänker att de borde kunna ske samtidigt eftersom om xi tex. är 6 så är xi större än 5 men mindre än 10?
Kan de inträffa samtidigt så är de inte oberoende.
Kolla definitionen. på oberoende
Arktos skrev:Kan de inträffa samtidigt så är de inte oberoende.
Kolla definitionen. på oberoende
Men du sa att disjunkta händelser är beroende? och i boken står det att disjunkta händleser inte kan inträffa samtidigt.
Så om de kan inträffa samtidigt så måste de ej vara disjunkta och de måste vara oberoende?
Om disjunkta händelser vet vi att
om den ena händelsen har inträffat så har den andra inte gjort det
Om oberoende händelser vet vi att
om den ena händelsen har inträffat
så vet vi därmed inget nytt om huruvida den andra har gjort det
Kolla denna tråd
https://www.pluggakuten.se/trad/oberoende-och-disjunkt/#post-b7061fe5-b47b-4f8b-8eb7-aabf00b4bce1
Arktos skrev:Om disjunkta händelser vet vi att
om den ena händelsen har inträffat så har den andra inte gjort detOm oberoende händelser vet vi att
om den ena händelsen har inträffat
så vet vi därmed inget nytt om huruvida den andra har gjort detKolla denna tråd
https://www.pluggakuten.se/trad/oberoende-och-disjunkt/#post-b7061fe5-b47b-4f8b-8eb7-aabf00b4bce1
Tack! nu har jag läst den tråden också:) men så om jag förstått det rätt:
*Oberoende händleser
-Är ej disjunkta
-Kan ske samtidigt
-om den ena har skett ger det ingen ny information om den andra skett eller ej
*Disjunkta händelser
-Är beroende
-Kan ej ske samtidigt
-Om den ena skett vet vi med säkerhet att den andra inte skett
*Händelser kan inte vara både disjunkta och oberoende
Knepigt detta!
Lätt att fastna i ordens mer vardagliga innebörd.
Men man vänjer sig,
som med andra facktermer som betecknas
med ord som i vardagslag har annan innebörd.
Kolla igen hur begreppen behandlas i din kursbok
Summan av den totala sannolikheten ska vara lika med ett, dvs så
Sant
Men hur beräknar du den sökta sannolikheten?
Arktos skrev:Knepigt detta!
Lätt att fastna i ordens mer vardagliga innebörd.Men man vänjer sig,
som med andra facktermer som betecknas
med ord som i vardagslag har annan innebörd.Kolla igen hur begreppen behandlas i din kursbok
Jo precis, jag blandar alltid ihop det när det kommer till oberoende och disjunkta:(
D4NIEL skrev:Summan av den totala sannolikheten ska vara lika med ett, dvs så
Tack!