bestäm och ange hypotenusan längd?

Jag skulle tro att de menar såhär: 

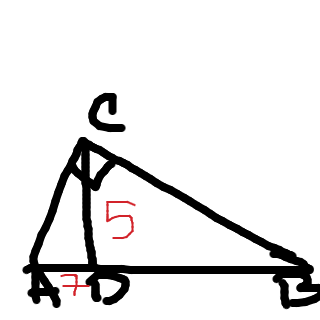
Börja med att rita upp en rätvinklig triangel enligt anvisningarna. Markera en punkt D på sidan AB. Rita höjden CD, markera att den skall föreställa rätvinklig och sätt ut vilka sträckor som är 5 respektive 7 längdenheter. Lägg upp bilden här när den är färdig, så skall vi kontrollera att den är riktig.

Jag löste den såhär.Dra från punkten D en rätvinklig linje mot AC kalla skärningspunkten P , dra ytterligare en rätvinklig linje mot BC kalla skärningspunkten O.  Trianglarna ADP,DCP,CDO ,DOB och ABC är likformiga trianglar. 

Det gäller ekvationssystemet $$\begin{gathered} {\left(AP\right)}^2+(DP{)}^2=49 \\ (DP{)}^2+(PC{)}^2=25 \end{gathered}$$

Samt att $\frac{7}{AP}=\frac{5}{DP}=AP=\frac{7DP}{5}$

Om du sätter in detta uttryck ovan i första ekvationen får du ekvation som du kan lösa

indhelpmathematica skrev:

Jag löste den såhär.Dra från punkten D en rätvinklig linje mot AC kalla skärningspunkten P , dra ytterligare en rätvinklig linje mot BC kalla skärningspunkten O.  Trianglarna ADP,DCP,CDO ,DOB och ABC är likformiga trianglar. 

Det gäller ekvationssystemet $$\begin{gathered} {\left(AP\right)}^2+(DP{)}^2=49 \\ (DP{)}^2+(PC{)}^2=25 \end{gathered}$$

Samt att $\frac{7}{AP}=\frac{5}{DP}=AP=\frac{7DP}{5}$

Om du sätter in detta uttryck ovan i första ekvationen får du ekvation som du kan lösa

hur ska man få ut längden DB med det där dock?

Pröva med trigonometri tex tan A = 5/7 osv...

nilson99 skrev:

indhelpmathematica skrev:

Jag löste den såhär.Dra från punkten D en rätvinklig linje mot AC kalla skärningspunkten P , dra ytterligare en rätvinklig linje mot BC kalla skärningspunkten O.  Trianglarna ADP,DCP,CDO ,DOB och ABC är likformiga trianglar. 

Det gäller ekvationssystemet $$\begin{gathered} {\left(AP\right)}^2+(DP{)}^2=49 \\ (DP{)}^2+(PC{)}^2=25 \end{gathered}$$

Samt att $\frac{7}{AP}=\frac{5}{DP}=AP=\frac{7DP}{5}$

Om du sätter in detta uttryck ovan i första ekvationen får du ekvation som du kan lösa

hur ska man få ut längden DB med det där dock?

Med likformighet. Från likformigheten mellan de två trianglarna $ADP \mathrm{och} \mathrm{DPC}$ och insättning i första ekvationen kan du hitta $AP$

$DP=\frac{5AP}{7}$

$(AP{)}^2+(DP{)}^2=49=(AP{)}^2+\frac{25(AP{)}^2}{49}=\frac{74(AP{)}^2}{49}\to \frac{49}{\sqrt{74}}$

Eftersom vinkeln $ADC \mathrm{är} \frac{\mathrm{\pi }}{2} (\mathrm{då} \det \mathrm{är} \mathrm{en} \mathrm{höjd}). \mathrm{Då} \mathrm{gäller} \mathrm{att} (\mathrm{AC}{)}^2=(\mathrm{AD}{)}^2+(\mathrm{DC}{)}^2=\to \sqrt{74}$

Likformighet ger $\frac{AP}{AC}=\frac{AD}{AB}=\frac{{\displaystyle \frac{49}{\sqrt{74}}}}{\sqrt{74}}=\frac{7}{AB}=AB=\frac{74}{7}$

indhelpmathematica skrev:

nilson99 skrev:

Visa föregående citat

indhelpmathematica skrev:

Jag löste den såhär.Dra från punkten D en rätvinklig linje mot AC kalla skärningspunkten P , dra ytterligare en rätvinklig linje mot BC kalla skärningspunkten O.  Trianglarna ADP,DCP,CDO ,DOB och ABC är likformiga trianglar. 

Det gäller ekvationssystemet $$\begin{gathered} {\left(AP\right)}^2+(DP{)}^2=49 \\ (DP{)}^2+(PC{)}^2=25 \end{gathered}$$

Samt att $\frac{7}{AP}=\frac{5}{DP}=AP=\frac{7DP}{5}$

Om du sätter in detta uttryck ovan i första ekvationen får du ekvation som du kan lösa

hur ska man få ut längden DB med det där dock?

Med likformighet. Från likformigheten mellan de två trianglarna $ADP \mathrm{och} \mathrm{DPC}$ och insättning i första ekvationen kan du hitta $AP$

$DP=\frac{5AP}{7}$

$(AP{)}^2+(DP{)}^2=49=(AP{)}^2+\frac{25(AP{)}^2}{49}=\frac{74(AP{)}^2}{49}\to \frac{49}{\sqrt{74}}$

Eftersom vinkeln $ADC \mathrm{är} \frac{\mathrm{\pi }}{2} (\mathrm{då} \det \mathrm{är} \mathrm{en} \mathrm{höjd}). \mathrm{Då} \mathrm{gäller} \mathrm{att} (\mathrm{AC}{)}^2=(\mathrm{AD}{)}^2+(\mathrm{DC}{)}^2=\to \sqrt{74}$

Likformighet ger $\frac{AP}{AC}=\frac{AD}{AB}=\frac{{\displaystyle \frac{49}{\sqrt{74}}}}{\sqrt{74}}=\frac{7}{AB}=AB=\frac{74}{7}$

vart fick du $\frac{74{\left(AP\right)}^2}{49}$ifrån