Bestäm minsta integral

Jag är osäker på vad du undrar, men om man säger t. ex. "bestäm b så att $b^2 + 3b + 7$ blir så litet som möjligt", förstår du vad som menas med det? 

Välkommen till Pluggakuten!

För att besvara den frågan behöver vi titta lite på vad det innebär att beräkna en integral inom ett visst intervall. Vi tar en slumpmässig funktion:

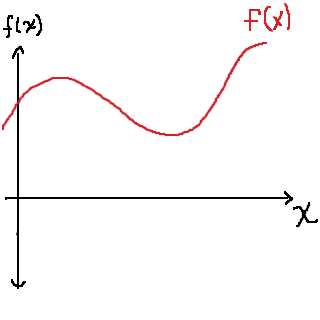
Beroende på hur funktionen ser ut i intervallet kommer arean under grafen vara olika stor:

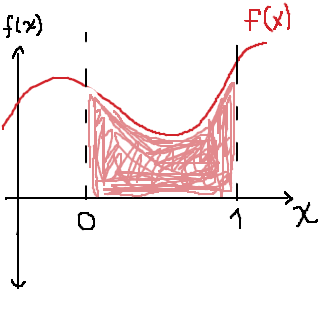
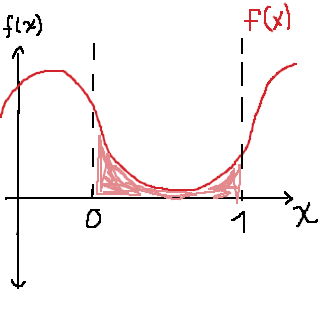
Integralens värde kommer därför att bero av a. Vi kan rita en graf över värdet av integralen av f(x), givet ett visst värde på a: 

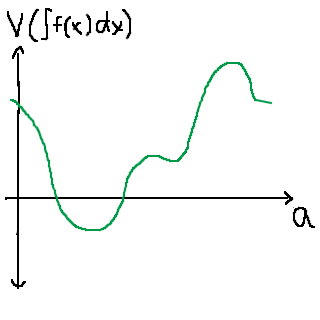
När vi vill hitta det minsta värdet på integralen kan vi därför derivera med avseende på a, och hitta minimi- och maxpunkter hos grafen. Eftersom vår funktion nu ger värdet på integralen, är vi därför hemma. Vi hittar ett visst a, som ger det minsta värdet på integralen. :)

Jag vet hur varje steg i uppgiften går till men jag fattar inte varför jag deriverar den primitiva funktionen för att försöka få fram nollställen, d.v.s vad säger minimipunkten egentligen?

Är det helt enkelt att grafen sjunker som lägst vid minimipunkten och att integralen (arean i intervallet) då blir så litet som möjligt

(Du glömde ett integraltecken i din fråga, eller hur?)

Bildligt så betyder uppgiften att du ska bestämma vilket värde $a$ska ha för att arean mellan funktionen $y={\left(x^2-ax\right)}^2$ och x-axeln, ska bli så liten som möjligt över intervallet $x=0$till $x=1$.

Rita funktionen i ett koordinatsystem för ett par olika värden på $a$så förstår du.

Legoland skrev:

Är det helt enkelt att grafen sjunker som lägst vid minimipunkten och att integralen (arean i intervallet) då blir så litet som möjligt

Ja precis! Och eftersom funktionen aldrig är negativ (pga exponenten 2), så är det arean mellan funktion och x-axel det är fråga om.

Tror jag fattar nu, så när jag deriverar min primitiva funktion så får jag det a-värde som genererar lägst y-värde?

Legoland skrev:

Tror jag fattar nu, så när jag deriverar min primitiva funktion så får jag det a-värde som genererar lägst y-värde?

inte lägst y-värde, utan minst area. Funktionens minimipunkt och minimipunkt hos storleken på arean under funktionen, är två helt olika saker.

derivera den uträknade integralen, och sätt lika med 0, så får du det värde som generar extremvärden för storleken på arean under grafen. Bästa att du studerar tecknet vid extrempunkten för att säkerställa att det är en minimipunkt också.