bestäm minsta avståndet (linjär algebra)
försöker beräkna denna med projektion men har fastnat
jag har gjort en vektor från origo till känd punkt P = (1,5)
om jag projicerar OP på linjen kommer det kortaste avståndet vara längden av OP - proj OP på linjen
men hur ska jag projicera på linjen när jag inte har något? jag kan ju skapa en egen vektor som finns på linjen men hur ska jag veta vilken jag ska projicera på ?
eller finns det enklare metoder för att beräkna denna?
Har du ritat? Här är en enkel skiss över situationen:
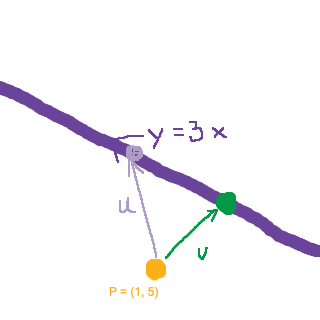
Den gröna punkten, Q, är den punkt på linjen som ligger närmast P. Du har som sagt hittat en vektor u, som går mellan P och en känd punkt på linjen y = 3x. Nu vill du projicera denna vektor u på en vektor parallell med linjen. Vilken vektor skulle du kunna ta? :)
pepparkvarn skrev:Har du ritat? Här är en enkel skiss över situationen:
Den gröna punkten, Q, är den punkt på linjen som ligger närmast P. Du har som sagt hittat en vektor u, som går mellan P och en känd punkt på linjen y = 3x. Nu vill du projicera denna vektor u på en vektor parallell med linjen. Vilken vektor skulle du kunna ta? :)
jag har inte hittat en vektor u som går mellan P och en känd punkt på linjen y = 3x. hur ska jag hitta den punkten eller väljer jag en punkt vilken som helst?
Du nämnde att du hittat en vektor mellan P och origo. Origo ligger på linjen y, och det fungerar därför utmärkt. :)
pepparkvarn skrev:Du nämnde att du hittat en vektor mellan P och origo. Origo ligger på linjen y, och det fungerar därför utmärkt. :)
jaha okej oj tänkte inte på det. som jag förstår behöver jag hitta riktningsvektorn som ligger på/parallell med linjen, men förstår inte hur jag hittar den? ska jag ta en annan punkt bara som ligger på linjen?
Du kan hitta vektorn genom att subtrahera två punkter på linjen, men det lättaste är att omvandla linjen till parameterform:
Vi har att y = 3x. Sätt att x = t. Då blir y = 3t. Allt som allt har vi linjen (x, y) = t(1, 3), där t är alla reella tal.
Riktningsvektorn är alltså (1, 3), och den kan du projicera på. :)
pepparkvarn skrev:Du kan hitta vektorn genom att subtrahera två punkter på linjen, men det lättaste är att omvandla linjen till parameterform:
Vi har att y = 3x. Sätt att x = t. Då blir y = 3t. Allt som allt har vi linjen (x, y) = t(1, 3), där t är alla reella tal.
Riktningsvektorn är alltså (1, 3), och den kan du projicera på. :)
yes okej jag är med, men när jag projicerar på den får jag fel svar eller så är det fel i min uträkning eller facit
riktningsvektorn r = (1, 3)
OP = (1, 5)
det bildar en triangel där projiceringen + m (som är den vektor vars längd är det minsta avståndet = OP
Det ser bra ut, och när jag plottar det i geogebra stämmer det. Vad säger facit?
pepparkvarn skrev:Det ser bra ut, och när jag plottar det i geogebra stämmer det. Vad säger facit?
aa okej, facit säger men det kanske är samma värde?
Prova faktorisera 10. :)
pepparkvarn skrev:Prova faktorisera 10. :)
haha herregud, tror jag suttit för länge med denna!
okej men då är jag med på upplägget för framtiden,
1) vi hittar en punkt på linjen och drar en vektor till angiven punkt
2) vi projicerar den på riktningsvektorn
3) minsta avståndet är längden av den vektor som fås av 1) - 2)
tusen tack för hjälpen!
Bingo! Varsågod! :)

