Bestäm minsta avståndet (LinAlg)
Hej!
Jag tycker att följande uppgift är ganska klurig:

Det korstaste avståndet mellan två linjer är en vinkelrät linje mellan dessa två. Men, hur ska jag hitta denna linje? Jag började fundera på om man kan ta normalerna för de båda linjerna och göra något med dessa, men sen slog det mig att vektorer ju har oändligt många normaler i R3.
Och del två i frågan där man vill bestämma de två punkter där avståndet är som minst: har man inte löst denna delfråga om man löst den första delen?
Linjerna har riktningsvektorer u = (2, 2, 1) och v = (1, 0, 1). Den kortaste sträckan mellan linjerna är vinkelrät mot båda, så om du bildar kryssprodukten u x v får du riktningen för denna linjestump.
Alltid en början.
Mogens skrev:Linjerna har riktningsvektorer u = (2, 2, 1) och v = (1, 0, 1). Den kortaste sträckan mellan linjerna är vinkelrät mot båda, så om du bildar kryssprodukten u x v får du riktningen för denna linjestump.
Alltid en början.
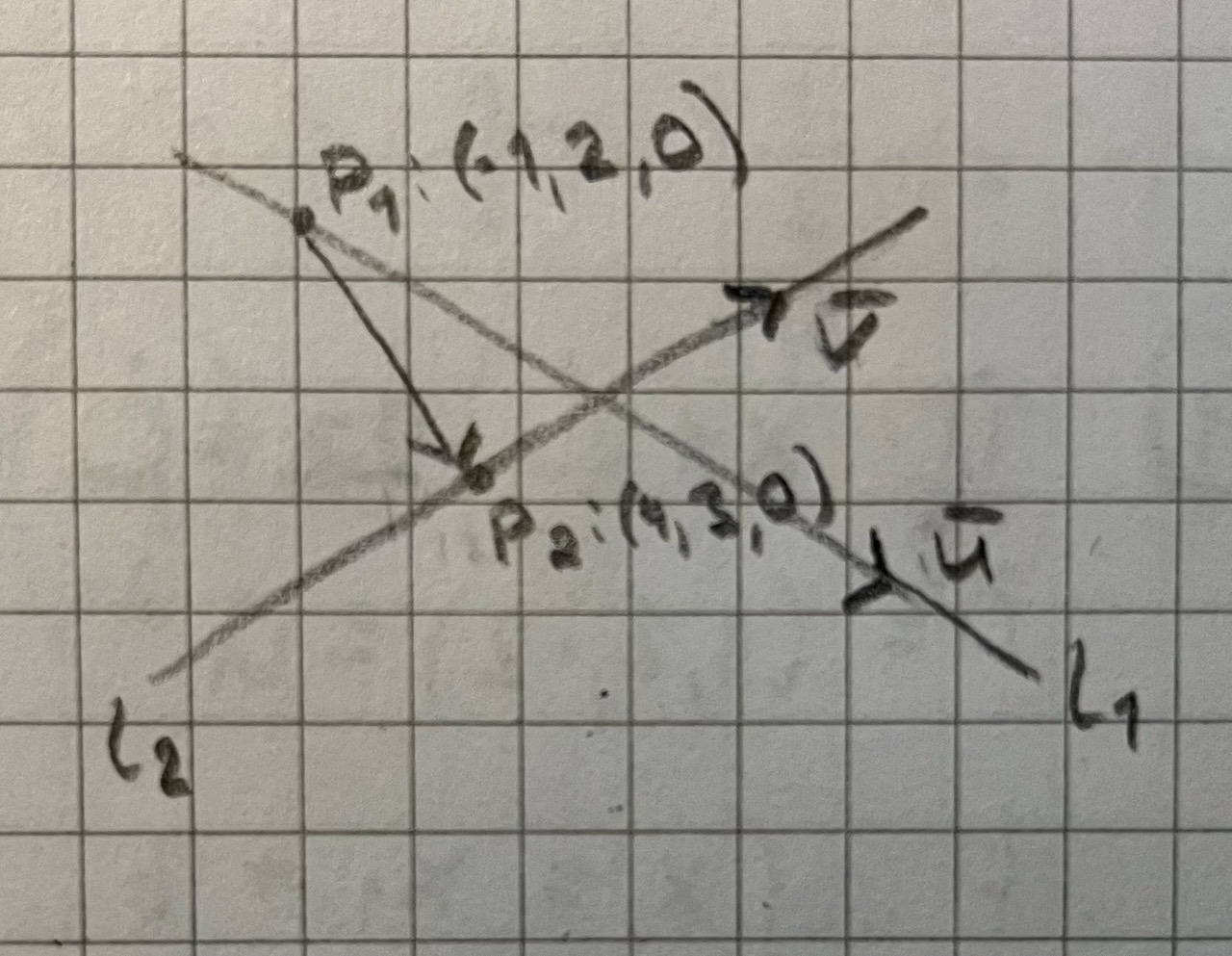
Okej! Jag beräknade kryssprodukten och fick (2, -1, -2). Målade också upp en bild där man ser linje L1 och L2. Jag tänker ju att denna kryssprodukt kommer peka rakt upp i pappret. Jag har också skrivit ut de punkter jag vet ligger på linjerna (framgick i frågan) och tagit fram vektorn (5,1,0) som går mellan dessa punkter (slutpunkt minus startpunkt).
Men, nu vet jag inte hur jag ska fortsätta. Nu slog mig också tanken att eftersom linjerna inte är parallella, så kommer de ju att korsa varandra i någon punkt, eller gäller enbart det i R2? För om så är fallet, så vore väl minsta avståndet 0 (i skärningspunkten)?
Jag snabbräknade uppgiften och fick ett orimligt svar. Men jag kan berätta min metod. Först dina frågor:
Nej linjerna möts troligen inte eftersom vi är i tredimensionella rummet. Tv flygplan som passerar varandra på olika höjd och med olika riktning kolliderar lyckligtvis inte.
Din figur ger ingen ledning.
Jag gjorde så här. En punkt på l1 har koordinaterna (–1+2s, 2+2s, s). (Men helst ser vi den som en vektor från origo till punkten, strunt i det nu.)
Från den punkten drar vi kryssproduktvektorn (2q, –q, –2q).
Den ska träffa en punkt på l2, dvs (4+t, 3, t). Det ger
(–1+2s+2q, 2+2s–q, s–2q) = (4+t, 3, t)
Tar du detta komponent för komponent har du ett ekvationssystem med tre ekvationer och tre obekanta som bör ha entydig lösning.
Vid närmare eftertanke, flygplanen var en dålig bild. Två båtar som rör sig med olika kurs över havet kan passera samma punkt utan att kollitera.
Mogens skrev:Jag snabbräknade uppgiften och fick ett orimligt svar. Men jag kan berätta min metod. Först dina frågor:
Nej linjerna möts troligen inte eftersom vi är i tredimensionella rummet. Tv flygplan som passerar varandra på olika höjd och med olika riktning kolliderar lyckligtvis inte.
Din figur ger ingen ledning.
Jag gjorde så här. En punkt på l1 har koordinaterna (–1+2s, 2+2s, s). (Men helst ser vi den som en vektor från origo till punkten, strunt i det nu.)
Från den punkten drar vi kryssproduktvektorn (2q, –q, –2q).
Den ska träffa en punkt på l2, dvs (4+t, 3, t). Det ger
(–1+2s+2q, 2+2s–q, s–2q) = (4+t, 3, t)
Tar du detta komponent för komponent har du ett ekvationssystem med tre ekvationer och tre obekanta som bör ha entydig lösning.
Tack för förklaringen! Jag hänger typ med, men tycker det är svårt. Jag hade förmodligen inte kommit på denna lösning på egen hand vid en tentaskrivning..! Hoppas jag slipper en sådan här uppgift. :)
Nu tycker jag du ska hoppas att det kommer en sådan här uppgift. Annars var ju min förklaring förgäves.
PS Jag tycker sådana här uppgifter blir mycket lättare om man skriver vektorer på kolonnform. Det blir smidigare övergång till ekvationssystem och man ser vad som händer.
Mogens skrev:Nu tycker jag du ska hoppas att det kommer en sådan här uppgift. Annars var ju min förklaring förgäves.
PS Jag tycker sådana här uppgifter blir mycket lättare om man skriver vektorer på kolonnform. Det blir smidigare övergång till ekvationssystem och man ser vad som händer.
Det har du rätt i: jag tar tillbaka det jag sa... :)

