Bestäm med central differenskvot f'(2) med 5 korrekta decimaler, då f(x)=2x*3^-x ?

Hur långt har du kommit? 

Dracaena skrev:

Hur långt har du kommit? 

Jag kan inte få fram f'(x). jag försökte använda n.x^n-1 men jag tänker nog fel. 

Du ska inte derivera i den här uppgiften, utan använda dig av central differenskvot.

dvs (f(2-h)-f(2+h))/2h

Tillägg: 31 maj 2022 18:32

Jag har råkat vända uttrycket fel

 (f(2+h)-f(2-h))/2h 

ska det vara

Ture skrev:

Du ska inte derivera i den här uppgiften, utan använda dig av central differenskvot.

dvs (f(2-h)-f(2+h))/2h

Tack, löst klart uppgiften.

Hur ska man tänka för att lösa denna uppgift? Jag förstår inte

Julialarsson321 skrev:

Hur ska man tänka för att lösa denna uppgift? Jag förstår inte

Vet du vad en central differenskvot är och hur den kan användas för att få ett närmevärde till en derivata vid ett specifikt x-värde?

Julialarsson321 skrev:

Hur ska man tänka för att lösa denna uppgift? Jag förstår inte

Jag kom fram till det svaret.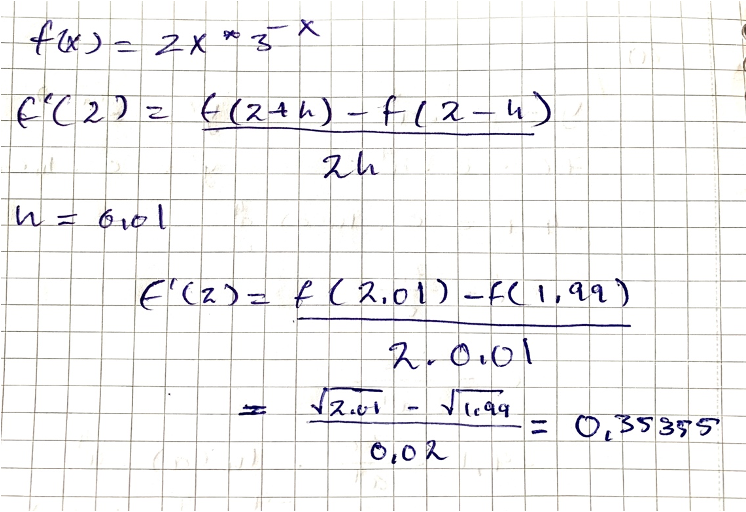

Hej!

Hur kom du till att h=0,01?

Jag fattar inte!

x.28.1 skrev:

Hej!

Hur kom du till att h=0,01?

Jag fattar inte!

Hej och välkommen till Pluggakuten!

Du ska bestämma f'(2) med 5 korrekta decimaler.

Ju mindre h är desto bättre närmevärde ger den centrala differenskvoten.

Gör så här:

Beräkna först värdet med h = 0,1

Beräkna sedan värdet med h = 0,01

Jämför decimalerna i dessa två värden. Om de 5 första decimalerna är lika så är du klar.

Annars får du gå vidare och beräkna värdet med h = 0,01.

Jämför decimalerna i detta värde med det tidigare värdet. Om de 5 första decimalerna är lika så är du klar, annars får du gå vidare med ännu mindre värde på h.

Och så vidare.

Om du vill ha mer hjälp så föreslår jag att du startar en ny tråd och ställer frågorna där. Då får du både snabbare och bättre hjälp.