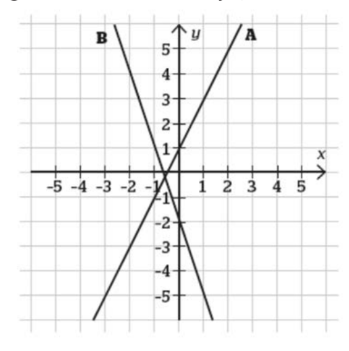
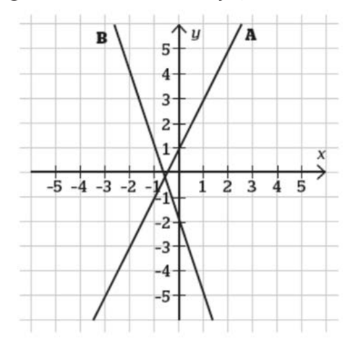
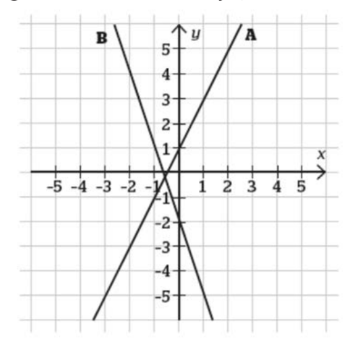
Bestäm linjernas ekvationer
Hej
Linje A har koordinaterna -0,5 , 1 och B har -0,6 , -2
Linje A: för varje steg åt höger jag går på x-axeln så blir y 3 steg större. dens punkter är -0,5 och 1.
x-värde: ändras från -0 förändringen är +1
sen vet hag inte hur jag ska göra för att räkna ut y-värdet.
Jag har försökt att beräkna båda linjers ekvationer och håller på att bli galen.
Jag förstår inte frågan. Har du en bild?
syns den nu?
ashe_ skrev:Hej
Linje A har koordinaterna -0,5 , 1 och B har -0,6 , -2
Nej, punkt A har koordinaterna -0,5 , 1 och punkt B har -0,6 , -2
Linje A: för varje steg åt höger jag går på x-axeln så blir y 3 steg större.
Nej, det stämmer inte. Titta igen.
dens punkter är -0,5 och 1.
x-värde: ändras från -0 förändringen är +1
sen vet hag inte hur jag ska göra för att räkna ut y-värdet.Jag har försökt att beräkna båda linjers ekvationer och håller på att bli galen.
Vad är frågan? Skall du skriva linjernas ekvationer?
Bubo skrev:
Nej, punkt A har koordinaterna -0,5 , 1 och punkt B har -0,6 , -2
Ingen av dessa punkter ligger på någon av de i uppgiften givna linjerna.
Vi behöver se hela uppgiften, även texten.
Bubo skrev:
Vad är frågan? Skall du skriva linjernas ekvationer?
ja
Uppgiften är:
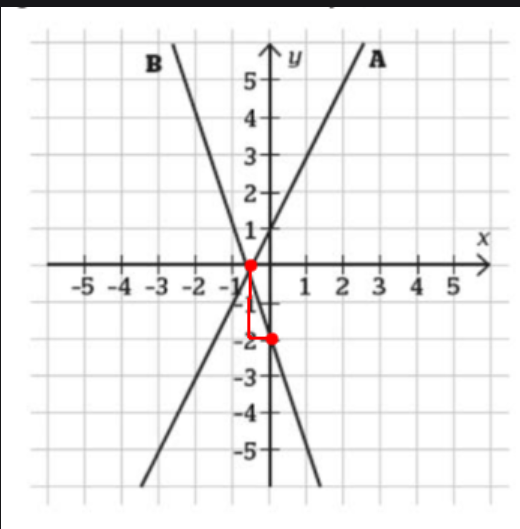
I diagrammet finns två räta linjer, A och B. Bestäm linjernas ekvationer.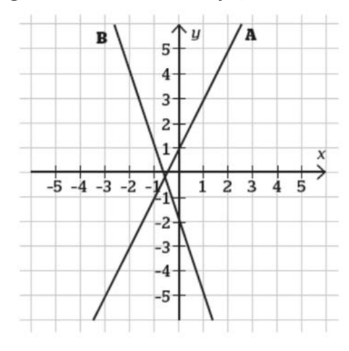
OK bra.
Vad vet du om räta linjens ekvation y = kx+m?
Vet du t.ex. vad k och m står för?
k är riktningskoefficient och motsvarar linjens lutning
m berättar om var linjen skär y-axeln
Yngve skrev:Bubo skrev:Nej, punkt A har koordinaterna -0,5 , 1 och punkt B har -0,6 , -2
Ingen av dessa punkter ligger på någon av de i uppgiften givna linjerna.
Tack. Det borde jag kontrollerat.
ashe_ skrev:k är riktningskoefficient och motsvarar linjens lutning
m berättar om var linjen skär y-axeln
OK bra det stämmer.
Vet du även hur du kan ta reda på k-värdet?
En parentes: vad ashe_ angav i första inlägget är var linjerna skär axlarna,
x-koordinaten för skärningen med x-axeln och motsvarande för y-axeln.
Yngve skrev:
OK bra det stämmer.
Vet du även hur du kan ta reda på k-värdet?
Ja det kan jag
Okej så jag har lugnat ned mig och tror jag har kommit någonstans med denna uppgift:
Linje A
y = kx + m (y = -1x + 1)
Lutningen k finner jag igenom att studera på vilket/vilka sätt stegen i x-led förhåller sig till stegen i y-led. För varje steg i x-led tas två steg i y-ledet för varje punkt längs linje A.
K-värdet innebär då en ökning av x-värdet med 1 och en ökning av y-värdet med 2. För varje steg åt höger jag går på x-axeln, blir y 2 steg större. Alltså blir y 2 steg större, när x blir 1 steg ett större. Det går 2x på varje y.
Sen vet jag inte hur jag ska göra. Jag vet inte ens om jag tänkt rätt.
Lite hjälp, någon?
Ja, linje A har k-värdet 2.
Välj en punkt som ligger på linjen. Nu vet du k, x och y i y = kx+m, så du kan beräkna m.
m läser du av i grafen så som du beskrev i #8 och rätt skrev i #13.
Men där angav du linje A som y = -1x + 1, fast du sedan skrev att k=2.
Louis skrev:m läser du av i grafen så som du beskrev i #8 och rätt skrev i #13.
m är alltså = 1?
Men där angav du linje A som y = -1x + 1, fast du sedan skrev att k=2.
är det korrekta svaret för linje A istället y = -2x + 1?
Nej, k=2 som du själv kom fram till. Ett steg åt höger, 2 steg uppåt.
En linje som har negativt k lutar som linje B.
m=1, ja.
y = 2x + 1?
Ja, det stämmer.
Så betyder det att A linjens ekvation är y = 2x +1?
Ja. Nu får du titta på linje B.
Börja gärna med att läsa av m.
Ok men är B:s koordinat -0,4?
m berättar om var linjen skär y-axeln
Var skär linje B y-axeln? Du kanske tittade på x-axeln.
Louis skrev:
Var skär linje B y-axeln? Du kanske tittade på x-axeln.
oj, linjen skär y-axeln på punkt -2
innwbär det då att dess koordinater är -0, -2?
Skärningspunktens koordinater (inte linjens) är (0,-2).
y-koordinaten är alltså -2.
Det betyder att m=-2.
Och så har vi k-värdet.
Louis skrev:
Skärningspunktens koordinater (inte linjens) är (0,-2).
y-koordinaten är alltså -2.
Det betyder att m=-2.Och så har vi k-värdet.
y = 0x + -2?
Hur fick du k till noll?
(k=0 innebär en vågrät linje.)
Börja någonstans på linjen där den har heltalskoordinater
(både linje A och linje B är ju så "snälla" att de går genom sådana punkter).
Gå ett steg åt höger, hur många steg uppåt/nedåt får du gå för att komma till linjen?
den går typ samma sak som i linje A om jag inte har fel: 2 ned och en till höger
Jag får det till 1 höger, 3 nedåt. Börja t ex vid skärningen med y-axeln.
Vilket k-värde får du av det?
här är ett exempel hur jag tänkt
Louis skrev:Jag får det till 1 höger, 3 nedåt. Börja t ex vid skärningen med y-axeln.
Vilket k-värde får du av det?
-3??
Men då börjar du i (-2/3, 0) och går 2/3 steg åt höger, 2 steg nedåt.
Det är enklare att börja i (0,-2) och gå 1 steg åt höger.
Innan jag hann posta kom ditt nästa svar. Ja, k=-3.
Så ekvationen för linje B blir?
hm.
y = -3x + -2
Ja. Som man skriver y = -3x - 2.
Det kan vara bra att upprepa stegningen för att se att man får samma resultat.
Alltså om linjen verkligen går så snyggt genom heltalspunkter.
Man kan också ta flera steg åt höger, se hur många steg man får gå i y-led och sedan dela med antalet steg i x-led.
Det här med att gå höger och uppåt/nedåt funkar bra på de här enkla linjerna.
Annars gäller att k = (y2-y1)/(x2-x1), där (x1,y1) och (x2,y2) är två punkter på linjen.
För linje A kan du testa den formeln med punkterna (-2,-3) och (2,5) som man kan läsa av på linjen.
Man får större noggrannhet om man väljer punkter som inte ligger så nära varandra.
Louis skrev:Ja. Som man skriver y = -3x - 2.
Alltså så är B linjens ekvation y = kx + m (y = -3x -2)?
Det kan vara bra att upprepa stegningen för att se att man får samma resultat.
Alltså om linjen verkligen går så snyggt genom heltalspunkter.
Man kan också ta flera steg åt höger, se hur många steg man får gå i y-led och sedan dela med antalet steg i x-led.
Det ska jag göra!
Det här med att gå höger och uppåt/nedåt funkar bra på de här enkla linjerna.
Jaha, då vet jag till nästa gång.
Annars gäller att k = (y2-y1)/(x2-x1), där (x1,y1) och (x2,y2) är två punkter på linjen.
Oj. Men åh herregud. Hjärnan gör ont bara av att kolla på allting.
För linje A kan du testa den formeln med punkterna (-2,-3) och (2,5).
Det ska jag komma ihåg.
För linje A:
k = (y2-y1)/(x2-x1)
k = (5-(-3))/(2-(-2)) = (5+3)/(2+2) = 8/4 = 2
Du börjar här i (-2,-3), går 4 steg åt höger och 8 steg uppåt för att komma till (2,5) på linjen. 8/4 = 2, k=2.
Täljaren: skillnaden i y-led, nämnaren: skillnaden i x-led.
Det funkar förstås också om koordinaterna inte är heltal.