Bestäm intervallret

Gissar du eller har du någon anledning till detta.

Var grafen med i uppgiften?

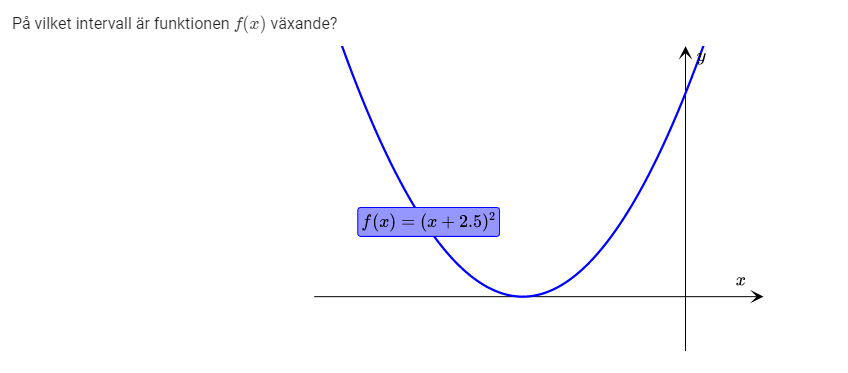
Ja, den var med, jag räknade minimipunkten och fick (2,5;0) alltså börjar den växa efter 2,5

Att funktionen f(x) är växande på intervallet [-2.5, $\infty$) betyder att om -2.5 $\le$ a < b så är f(a) $\le$ f(b). Är detta uppfyllt?

Jag fattar inte riktigt det du menar

Svaret ska vara $x\geq-2,5$.

Detta eftersom funktionsvärdet hela tiden växer (egentligen inte minskar) då vi förflyttar oss "åt höger" från $x=-2,5$. "Växandet" börjar alltså redan vid $x=-2,5$.

Om det fortfarande är oklart så kan vi förklara med hjälp av de begrepp du har stött på i kursen. Kan du ladda upp en bild på hur definitionen av en växande funktion ser ut i din bok/ditt studiematerial?

Jag förstår vad du menar, tack så mycket för hjälpen

Bayan Ali skrev:

Jag fattar inte riktigt det du menar

Titta på definitionen på Wikipedia.

I vårt fall så är f(x) = (x+2.5)².

Antag nu att vi har två tal a och b som uppfyller  -2.5$\le$ a < b.

Då gäller det att 0 $\le$ a + 2.5 < b +2.5.

Vi tittar nu på värdet av f(b) - f(a). Notera att om f(b) - f(a) > 0 så är det det samma som att f(a) < f(b).

f(b) - f(a) = (b+2.5)² - (a+2.5)² = (konjugatregeln) = (b-a)(a+2.5+b+2.5). Notera att båda faktorerna i det sista uttrycket är positiva, dvs (b-a) är positiv och (a+2.5+b+2.5) positiv, så produkten är också positiv eftersom produkten av två positiva tal är ett positivt tal (axiom).

Således är f(b)-f(a)>0 och därmed är f(a) < f(b). Således är funktionen f växande på intervallet [-2.5, $\infty$), f är till och med strängt växande på intervallet.