Bestäm golvarean för maximal volym
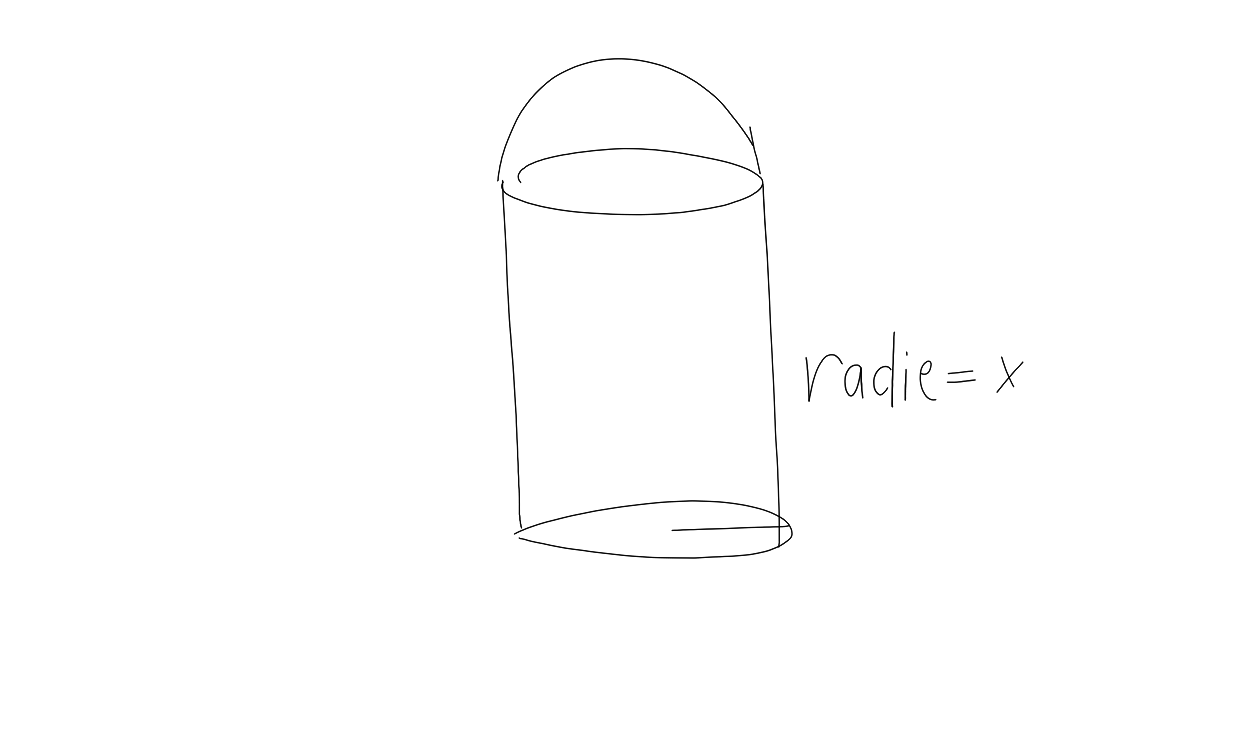
Fråga: av 70 m2 plåt ska den byggnad som bilden visar byggas. Plåten ska räcka till cylinderns mantelyta, halvklotet och det cirkelrunda golvet. Bestäm golvarean då byggnadens volym är maximal.
Svar: 14m2
Min halv-färdiga lösning:
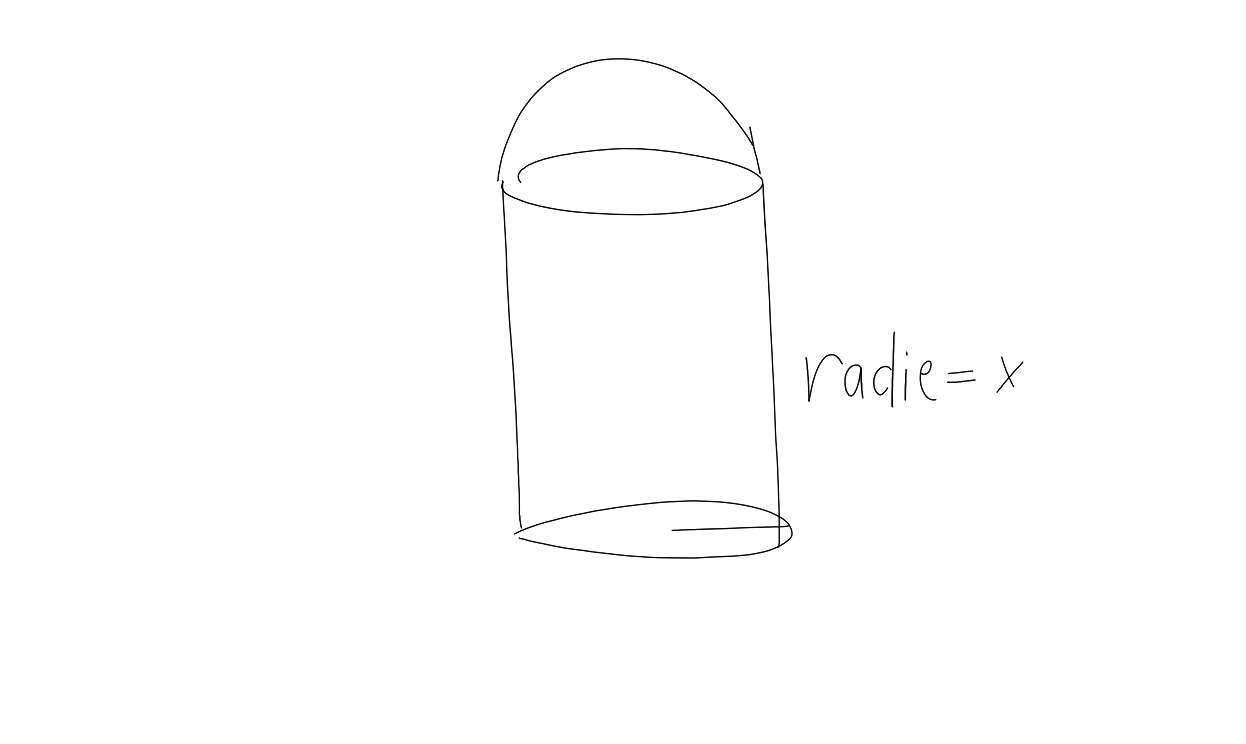
Volym v = x^2πh+(2πx³)/3
f(x)=70m²=2xπh+2πx²+x²π
lös ut h för att se hur h beror av x:
2xπh=70-2πx²-x²π
Dividera på 2xπ:
h=(35/xπ)-1,5x
volym v=x²π*((35/xπ)-1,5x)+(2πx³)/3
= 35x-1,5x³π+(2πx³)/3
v'(x)=35-4,5x²π+2πx²
det är när jag ska sätta v'(x)=0 som jag stöter på problemet. Jag kan ju inte använda pq formeln pga att det finns 2 stycken x² och de två termerna kan jag väl inte addera. Har lite brainfreeze, skulle vara tacksam för svar!
sauisen skrev:Fråga: av 70 m2 plåt ska den byggnad som bilden visar byggas. Plåten ska räcka till cylinderns mantelyta, halvklotet och det cirkelrunda golvet. Bestäm golvarean då byggnadens volym är maximal.
Svar: 14m2
Min halv-färdiga lösning:
Volym v = x^2πh+(2πx³)/3
f(x)=70m²=2xπh+2πx²+x²π
lös ut h för att se hur h beror av x:
2xπh=70-2πx²-x²π
Dividera på 2xπ:
h=(35/xπ)-1,5x
volym v=x²π*((35/xπ)-1,5x)+(2πx³)/3
= 35x-1,5x³π+(2πx³)/3
v'(x)=35-4,5x²π+2πx²
det är när jag ska sätta v'(x)=0 som jag stöter på problemet. Jag kan ju inte använda pq formeln pga att det finns 2 stycken x² och de två termerna kan jag väl inte addera. Har lite brainfreeze, skulle vara tacksam för svar!
Testa att faktorisera ut x2 i de två termerna
0=35-x²(4,5π+2π)
Vad gör jag nu?
Förenkla.
Laguna skrev:Förenkla.
0=35-x²(6,5π)
?
Hej,
Får du använda digitala hjälpmedel, dvs. miniräknare eller grafritare?
Du har x2 = 35 / (6,5 pi)
x blir isåfall 1,3... då den inte kan vara negativ.
men sätter jag in den i x²*pi som är formeln för golvarean blir det fel svar
Även när jag beräknar f''(x)=9*x*pi+4*pi*x, får jag ett positivt värde vilket menar att det är en minpunkt.
Enligt grafritaren ska svaret vara 2,11. Dock vet jag inte hur jag ska komma fram till svaret algebraiskt
I början har du skrivit -4,5 och +2 i uttrycket för v'(x), men sen har det blivit plus på båda.
Laguna skrev:I början har du skrivit -4,5 och +2 i uttrycket för v'(x), men sen har det blivit plus på båda.
precis, det blev fel där men det leder mig ändå till fel svar när jag ska beräkna golvarean.

Om -4,5 + 2 är rätt så är 6,5 inte rätt.
Laguna skrev:Om -4,5 + 2 är rätt så är 6,5 inte rätt.
tack så mycket! du räddade mig från ett två-dagars lidande.