Bestäm funktionernas eventuella lokala extrempunkter och terrasspunkter
f(x)=0,5x^3-0,6
Jag får funktionens derivata till 0 och andra derivata till 0 (kanske har fel) men hur ska jag veta om det är en terrass eller inte?
Nästan där!
Vilka extrempunkter får du när du deriverar f(x)?
f'(x)=1,5x2
1,5x2=0
x=0
f(0)=-0,6
Okay! Du har fått fram att extrempunkten är (0, -0.6).
Det som är grejen med terasspunkter är att de är ganska svåra att hitta. Jag menar så här:
Efter du tar andra derivatan, dvs beräknar f''(x) [som blir f''(x) = 3x i detta fall], brukar man sätta in extrempunkterna och se om f''(x) blir större än eller mindre än noll.
Om f''(c) > 0, är c en minimipunkt; där c är en extrempunkt
Om f''(c) < 0, är c en maximipunkt; där c är en extrempunkt.
Däremot blir det lite knepig om f''(c) = 0. Detta är för att vi kommer inte då veta om c är en minima/maximipunkt. Ta till exempel denna graf:
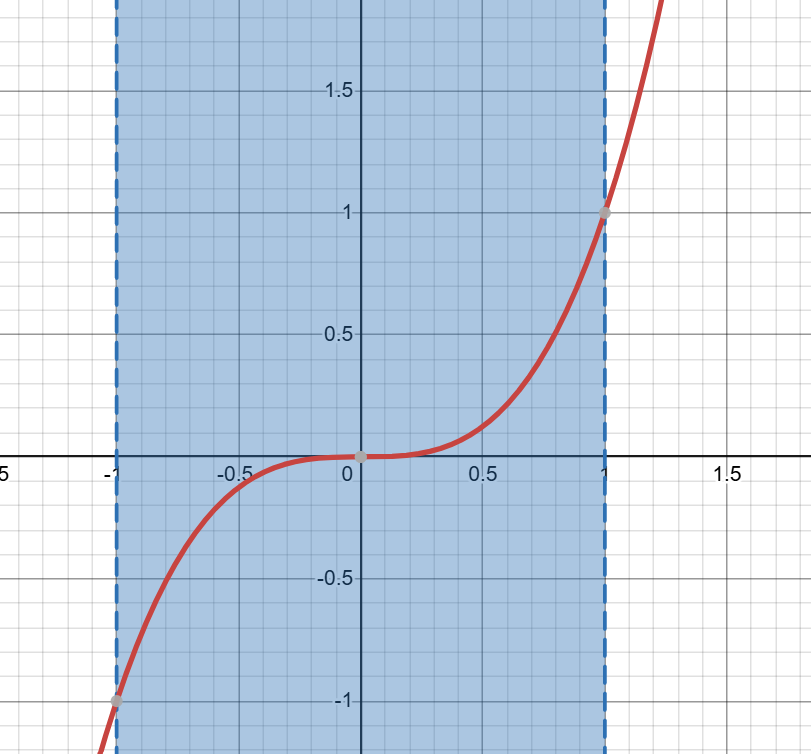
Funktionen är helt enkelt x^3, men med en begränsning mellan -1 < x < 1.
x = 0 i detta fall är en extrempunkt, men varken det minsta eller det största värdet. I detta fall blir alltså x = 0 en terasspunkt.
När du tar f''(0) = 3*0 = 0, så får du inte så mycket information från det, man kan inte dra en slutsats om punkten från denna derivata-undersökningen. Man säger alltså att undersökningen är "inconclusive"
källa: Second Derivative Test | Calculus III
Det bästa du kan göra i det här fallet är att ta grafen av funktionen och se om punkten är en terasspunkt eller inte...
Om det finns andra metoder att veta om en extrempunkt är just en terasspunkt så vet jag inte riktigt. Kanske någon som är mer vettigt kan bidra då. Men jag har inte sett någon riktig analytisk metod alls på gymnasiematten, för att kunna veta om en punkt är en terasspunkt eller inte.
Kanske inte det bästa svaren jag har gett hittils, men jag själv skulle vilja lära mig om det finns metoder för att kunna bestämma det i alla fall :D
Kan man inte använda sig av ett teckenschema för att lösa ut det?
Bra svar!
Jag vill reda ut begreppen lite här.
En terrasspunkt är inte en extrempunkt eftersom funktionsvärdet i en terrasspunkt inte är det mest extrema värdet i en omgivning av punkten.
Det finns ett fungerande gemensamt namn för minimi-, maximi- och terrasspunkter, nämligen stationära punkter.
Punkter där förstaderivatan är lika med 0 kallas alltså stationära punkter. Dessa kan vara minimi-, maximi- eller terrasspunkter.
Jacklidb skrev:Kan man inte använda sig av ett teckenschema för att lösa ut det?
Bra svar!
Jo, det är helt rätt.
Om både första- och andraderivatan är lika med 0 i en punkt så kan vi t.ex. använda en teckentabell för att bestämma den stationära punktens karaktär.
Yngve skrev:Jacklidb skrev:Kan man inte använda sig av ett teckenschema för att lösa ut det?
Bra svar!
Jo, det är helt rätt.
Om både första- och andraderivatan är lika med 0 i en punkt så kan vi t.ex. använda en teckentabell för att bestämma den stationära punktens karaktär.
Skulle du kunna ta ett exempel på hur man kan använda teckentabell? Jag har aldrig stött på metoden innan, eller behövt använda det riktigt. Kanske i denna scenario, så kan jag kanske förstå?
Hej allihopa!
Först ville jag bara säga förlåt för fel användning av begrepp. Jag visste att begreppet på engelska hette "criticial points", men trodde att översättningen till svenska blev då extrempunkter. Jag ber om ursäkt :D!
shkan skrev:
Skulle du kunna ta ett exempel på hur man kan använda teckentabell? Jag har aldrig stött på metoden innan, eller behövt använda det riktigt. Kanske i denna scenario, så kan jag kanske förstå?

Yngve skrev:shkan skrev:Skulle du kunna ta ett exempel på hur man kan använda teckentabell? Jag har aldrig stött på metoden innan, eller behövt använda det riktigt. Kanske i denna scenario, så kan jag kanske förstå?
Tack Yngve! Jag har greppat idén nu.


