Bestäm förhållandet
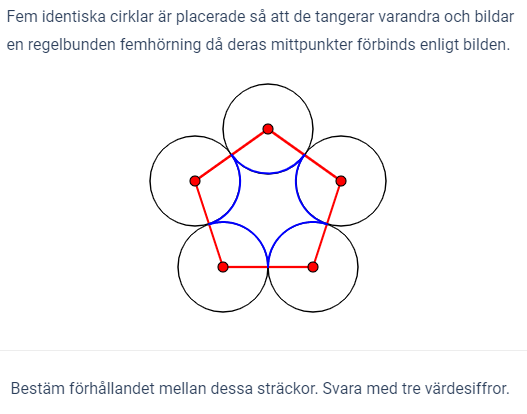
Röd = 2r5 = 10r = 10
Blå = 5(π120)180 = 10π/3
röd/blå = 3/π
tre värde siffror = 0.95 men det blir fel
Titta igen på beräkningen av bågarnas längd.
(Man kallar väl inte bågar för sträckor som de gjort i uppgiften?)
Och förklara hur du tänkt.
Du antar att radien är 1 och det kan du göra, men du bör förklara det med,
inte bara skriva 10r = 10. Fast att behålla r (som förkortas bort på slutet) gör lösningen tydligare.
Så att man t ex förstår att här handlar det om cirkelns omkrets.
Det är bra att skriva så att lösningen är lätt att följa för andra.
0,95 är två värdesiffror.
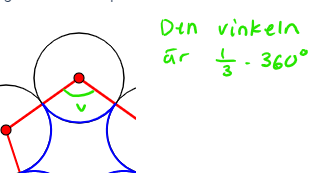
Hur fick du vinkeln till 120o?
Jag tänkte 360/3
Vinklarna i femhörningen är 540/5 = 108 grader.
Men det är enklare att tänka på vinkelsumman som 540/360 = 1,5 varv.
Summan av båglängderna blir då 1,5*2r.
Jag tänkte inne i cirkeln, för den utgör 1/3 del av cirkeln
Hänger inte med. Vad är 1/3 av vad?
Varje blå båge är inte 1/3 av cirkelns omkrets utan 108/360.
Nu skrev vi samtidigt. Nej, det stämmer inte, se #7 och #5.
Vinkelsumman i en femhörning är 540o.
Du kan dela upp den på tre trianglar: 3*180o.
Okej, jag hänger med nu. Jag får 10r/3πr tack
Jag fastnar dock på nästa delfråga.
Vad blir förhållandet då antalet cirklar i figuren går mot oändligheten? Svara exakt.
Jag får uttrycket 2n2/π(n-2) där n ska gå mot oändligheten, minns dock inte hur det var man skulle göra efter detta med sådana frågor
Det bör bli 2n i täljaren. Annars skulle uttrycket gå mot oändligheten.
Vad får uttrycket då för gränsvärde när n går mot oändligheten?
Jag tänker att det borde bli 2n2 eftersom de blåa är 180r(n-2)/n jag delar med n för att få veta hur stor varje vinkel är. Det röda är 2nr
2nr/(180r(n-2)/n) = 2n2r/(180r(n-2)) = 2n2/(180(n-2))
jag delar med n för att få veta hur stor varje vinkel är.
Men du stannar där och det innebär att du bara räknar en båge.
(n-2)*180 är summan av vinklarna, (n-2)/2 är antalet varv.
Summan av båglängderna är 2r(n-2)/2 = r(n-2).