Bestäm F(x) om f(x)=e^x/1+e^x och F(0)=ln8

Jag är osäker på vad du frågar om, vad jag kan se så har du gjort helt rätt.

Jag får räkna själv helt enkelt, det är inte mitt svar. Fick det på en hjälp grej i skolan och ville mest få en tolkning på vilka delar man bör kunna för detta men tack ändå.

Det viktigaste här att vet detta sambandet: 

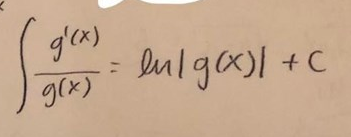
Annars får du integrera själv, vilket inte är hela världen så länge du vet hur substitution fungerar. :)

Exempelvis med $u=e^x+1$ så fås; 

$\displaystyle \int \dfrac{1}{u} du = \ln |u| +C=\ln |e^x+1|+C$

Jo, sisådär, får räkna och nöta. Kanske lite dum fråga men hur funkade detta sambandet. Har nog lite hjärnsläpp nu. Tack för svar! :)

Det är en direkt konsekvens av kedjeregeln.

I vanliga fall så har vi har $(\ln x)^\prime = \dfrac{1}{x}$, men detta är pga att inre derivatan är $1$, eller hur? Kedjeregeln säger att om vi har en sammansatt funktion så fås derivatan som:

$(f \circ g)^\prime = f^\prime (g(x))g^\prime (x)$

I ditt fall har vi:

$f(x) = \ln x$

$g(x)=e^x+1$

$h(x)= f \circ g$

Vi vet redan att $f^\prime (x) = \dfrac{1}{x}$, så att $f^\prime (g(x)) = \dfrac{1}{e^x+1}$ och sedan har vi $g^\prime (x)$ kvar. 

Vi har alltså: $h'(x)=\dfrac{g^\prime (x)}{g(x)}$

Wow tack! Hänger inte med helt men ska nöta, har massa luckor att ta igen

Vilken del hänger du inte med på? :)

Du får gärna fråga om det är något som ser konstigt ut eller om det är något steg som är oklart?

Koncepten här som du behöver vara bekväm med:

• Kedjeregeln $(3)$
• Sammansatta funktioner $(2)$
• Derivata $(1)$

Skrev de i fel ordning, men gå efter numreringen.

Tack för länkarna! Jo, nu lossna det, fastna på derivatan av ln x men tittar på ett bevis nu. Fastnar på basics och hur saker hänger ihop ibland. Får fråga massa bara. Tack så många för tiden du la på detta!

Ingen som helst fara. :)

Det finns ett ganska snyggt bevis med hjälp av kedjereglen av derivatam av ln x